Постройте график функции
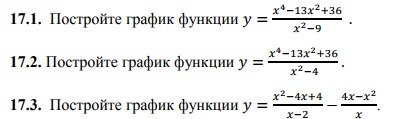
Ответы
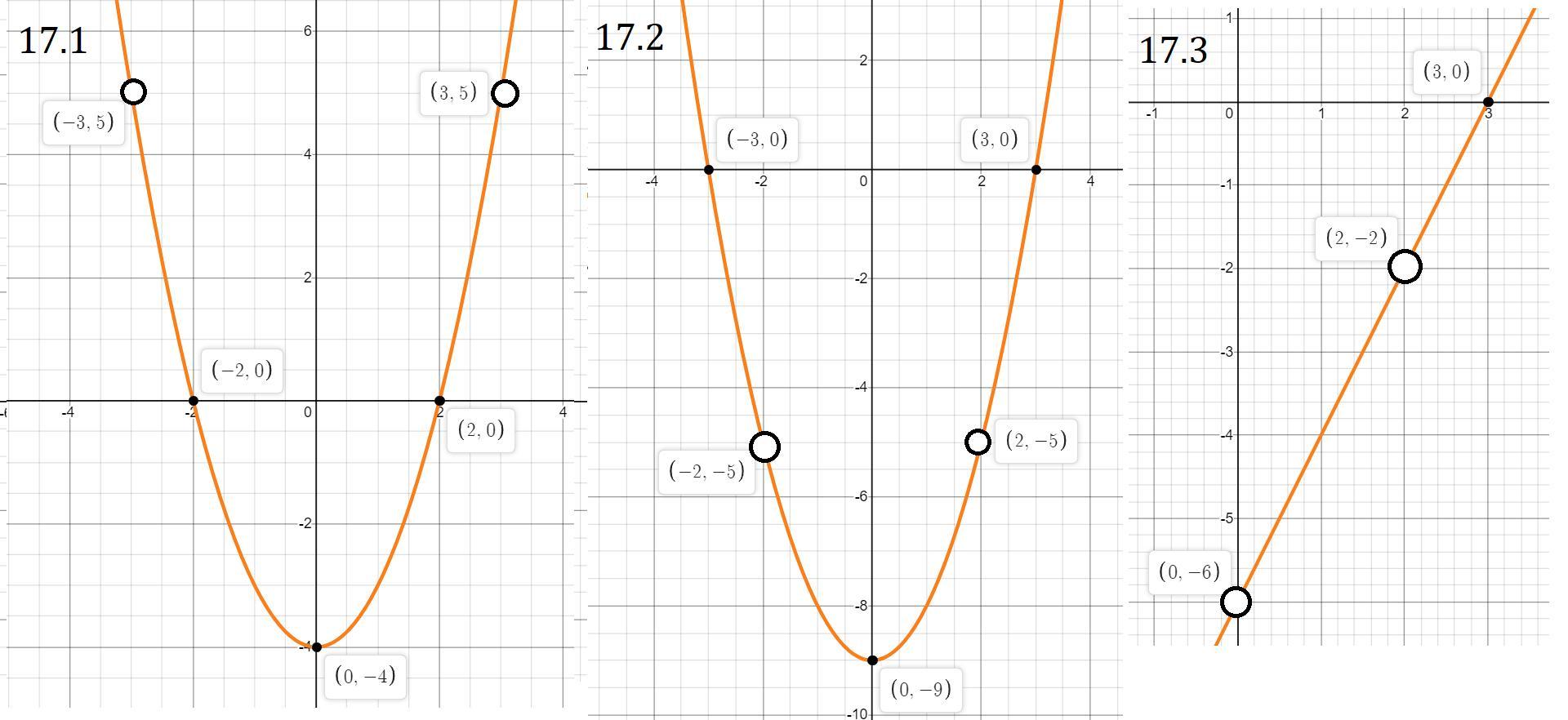
17.1
Исследуем функцию
Это парабола, ветви которой направлены вверх, координаты вершины (0;-4), её нули (-2;0),(2;0) пересекает ось Оу в точке (0;-4), построим параболу по трём точкам (вершина и нули), а затем выкалим точки, при которых первоначальная функция не определена.
Смотри вниз.
17.2
Исследуем функцию
Это парабола, ветви которой направлены вверх, координаты вершины (0;-9), её нули (-3;0),(3;0) пересекает ось Оу в точке (0;-9), построим параболу по трём точкам, а затем выкалим точки, при которых первоначальная функция не определена.
Смотри вниз.
17.3
Получившиеся функция, это уравнение прямой, построим прямую по двум точкам - (0;-6),(3;0) они же являются точками пересечения с осями координат, далее выкалим точки, при которых первоначальная функция не определена.
Смотри вниз.