Question

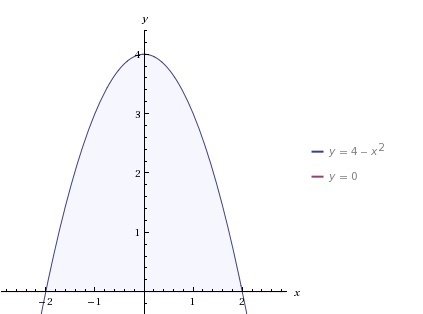
Вычислить площадь фигуры, ограниченную линиями y=4- x2 и y=0

Answer 1

Уравнение задает параболу, ветви которой направлены вниз, вершина находится в точке(0;4), парабола симметрична относительно оси ординат и пересекает ось абсцисс в точках(-2;0) и (2;0). 

Площадь фигуры находится через определенный интеграл в пределах от 0 до 2 с последующим удвоением площади.

S=2* ∫(4-х^2)dx=2*(4x-x^3/3) в пределах от 0 до 2 =

=2*(8-8/3)=32/3=10,(6).

Ответ:   

10,(6) кв. ед..