Предмет: Математика,
автор: tatijana
уравнение с параметром. 25 баллов
Приложения:
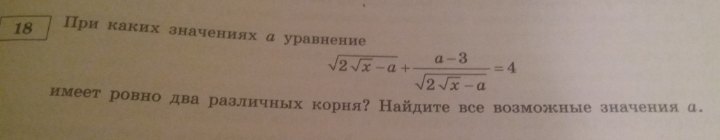
Ответы
Автор ответа:
0
При каких значениях а уравнение

имеет ровно два корня?
Решение:
Сделаем замену переменных

Очевидно что при любом положительном значении y переменная х будет иметь единственное значение. Покажем это



Следовательно, чтобы исходное уравнение имело ровно два корня необходимо чтобы уравнение

имело ровно два положительных корня y₁>y₂>0.
Так как у не равен нулю то умножим обе части уравнения на у.
y² + a - 3 = 4y
y² - 4y + a - 3 = 0
Получили квадратичное уравнение.
Данное уравнение имеет два корня если его дискриминант больше нуля.
D = (-4)² - 4*(a - 3) = 16 - 4a + 12 = 28 - 4a = 4(7 - a)
D > 0
7- a >0
a < 7
Корни уравнения


Проверим условие, что корни должны быть положительными


7 - a < 4
a > 3
Следовательно исходное уравнение имеет ровно два корня при всех значениях параметра а∈(3;7)
Ответ: а∈(3;7)
имеет ровно два корня?
Решение:
Сделаем замену переменных
Очевидно что при любом положительном значении y переменная х будет иметь единственное значение. Покажем это
Следовательно, чтобы исходное уравнение имело ровно два корня необходимо чтобы уравнение
имело ровно два положительных корня y₁>y₂>0.
Так как у не равен нулю то умножим обе части уравнения на у.
y² + a - 3 = 4y
y² - 4y + a - 3 = 0
Получили квадратичное уравнение.
Данное уравнение имеет два корня если его дискриминант больше нуля.
D = (-4)² - 4*(a - 3) = 16 - 4a + 12 = 28 - 4a = 4(7 - a)
D > 0
7- a >0
a < 7
Корни уравнения
Проверим условие, что корни должны быть положительными
7 - a < 4
a > 3
Следовательно исходное уравнение имеет ровно два корня при всех значениях параметра а∈(3;7)
Ответ: а∈(3;7)
Похожие вопросы
Предмет: Литература,
автор: mamedlinarmin312
Предмет: Другие предметы,
автор: gorobecviktori41
Предмет: Английский язык,
автор: wseolyx
Предмет: Геометрия,
автор: Anastasya28