Предмет: Математика,
автор: tatijana
уравнение с параметром. 25 баллов:)
Приложения:
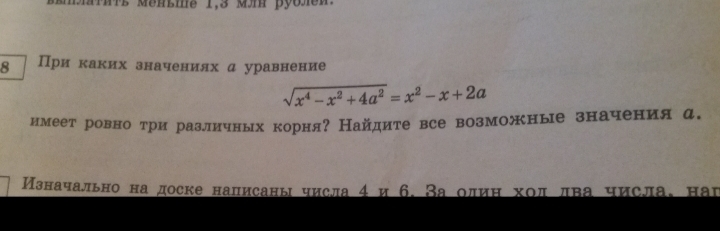
Ответы
Автор ответа:
0
При каких значениях параметра а уравнение
Имеет три различных корня
Решение: при x² - x + 2a <0 уравнение не имеет корней
При x² - x + 2a ⩾ 0 обе части уравнения можно возвести в квадрат.
x⁴ - x² + 4a² = x⁴ + x² + 4a² - 2x³ + 4ax² - 4ax
2x³ - 2x² - 4ax² + 4ax = 0
x³ - x² - 2ax² + 2ax = 0
x²(x - 2a) – x(x - 2a) = 0
(x - 2a)*x*(x - 1) = 0
x₁ = 0; x₂=1; x₃ = 2a
Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа x₁,x₂,x₃ были различными и для каждого из этих чисел выполнялось условие x₂ - x + 2a ⩾ 0.
Для х₁ = 0 x² - x + 2a = 2a ⩾ 0 ⇔ a⩾0
Для х₂ = 1 x² - x + 2a = 2a ⩾ 0 ⇔ a⩾0
Для х₃ = 2a x² - x + 2a = 4a² - 2a + 2a = 4a²⩾0 ⇔ a⩾0 a<0
Следовательно уравнение имеет три корня для всех значений параметра a∈(0;0,5)U(0,5;+∞)Ответ: a∈(0;0,5)U(0,5;+∞)
Автор ответа:
0
Вначале написал в ответе (0;1)U(1+oo). Этот ответ не правильный так как х=2а. А 2а не должен быть равен 1.
Автор ответа:
0
0 меньше а меньше 0.5; 0.5 меньше а меньше +бесконечность
Автор ответа:
0
Если 2а=1(при а =0,5) то получаться 2 ответа.
Автор ответа:
0
Понятно или нет???
Автор ответа:
0
понятно!!!
Похожие вопросы
Предмет: Английский язык,
автор: natalkalemberg20178
Предмет: Литература,
автор: mamedlinarmin312
Предмет: История,
автор: di56nisssssssss
Предмет: Химия,
автор: елена794470
Предмет: Алгебра,
автор: mariyamytr