Предмет: Математика,
автор: BJIADA
Решите неравенство , пожалуйста
Приложения:
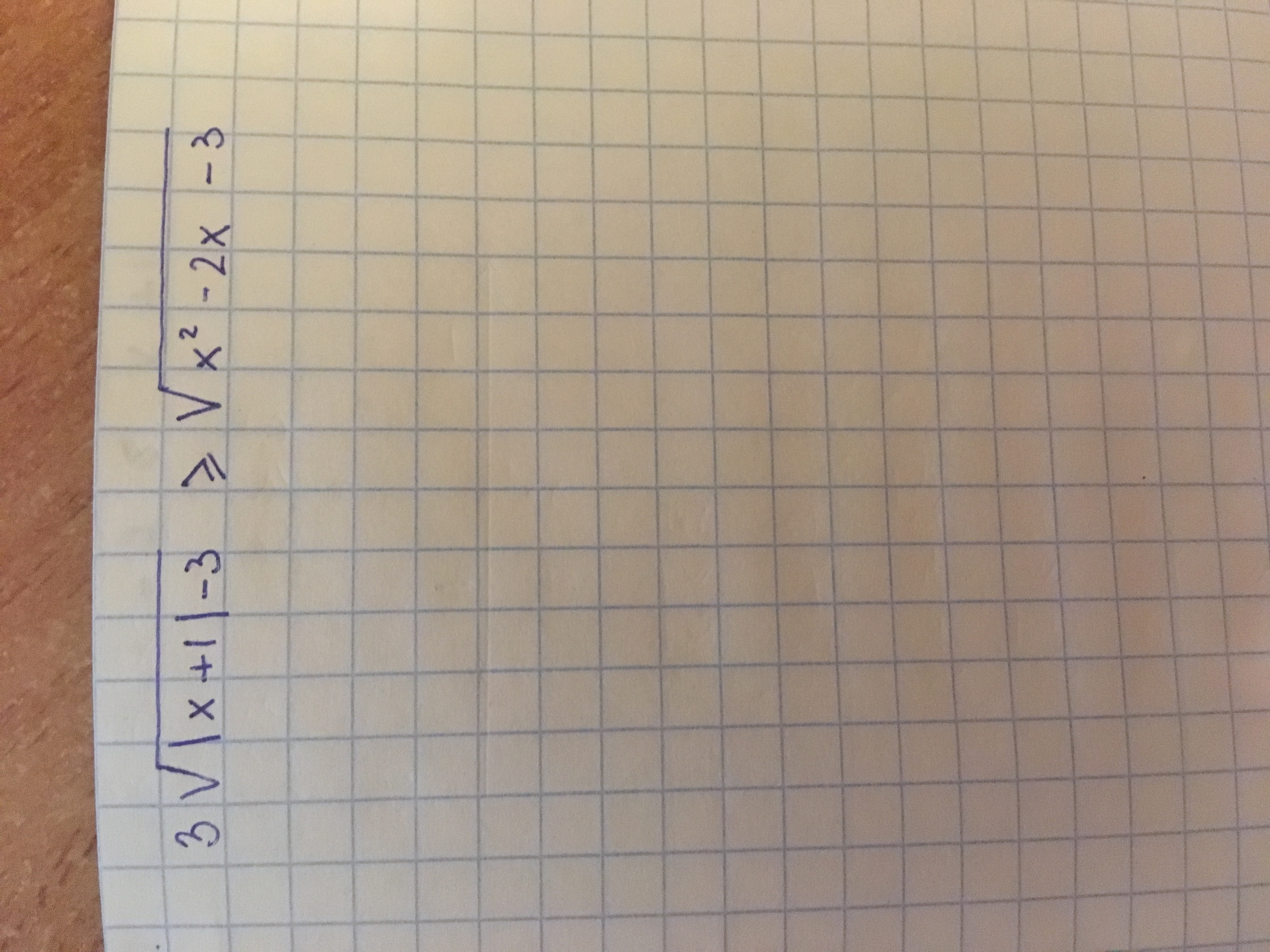
Ответы
Автор ответа:
0
task/27212683
---------------------
3√ ( |x+1| - 3) ≥ √ (x² - 2x - 3)
----------------------------------------
ОДЗ : { |x+1| - 3 ≥ 0 , x² -2x - 3 ≥ 0 .⇔ { |x+1| ≥ 3 , (x+1)(x-3) ≥ 0 . ⇔
|x+1| ≥ 3 ⇔ [ x+1 ≤ - 3 , x+1 ≥ 3 ⇔ [ x ≤ - 4 , x ≥ 2 .
и
(x+1)(x - 3) ≥ 0 ⇔ [ x ≤ - 1 , x ≥ 3.
/////////////////////////////// [ - 4 ] ------------------[2] ////////////////////////////////////////
///////////////////////////////////////////////////[ -1] ---------------- [3] ////////////////////////
x ∈( - ∞ ; - 4 ] ∪ [ 3 ; ∞).
-------------------------------
9|x+1| - 27 ≥ x² -2x - 3 ;
x² - 2x - 9|x+1| + 24 ≤ 0 ;
-------
a)
x ∈ ( - ∞ ; - 4 ]
x² - 2x + 9(x+1) + 24 ≤ 0
x² +7x + 33 ≤ 0 ⇔(x+3,5)² +20,75 ≤ 0 ⇒ x ∈ ∅ .
-------
б)
x ∈ [ 3 ; ∞)
x² - 2x - 9(x+1) + 24 ≤ 0 ;
x² -11x + 15 ≤ 0 ; * * * x₁= (11- √61)/2 , x₂ =(11+√61) / 2 * * *
x ∈ [ (11- √61)/2 ; (11+√61) / 2 ] * * * x ∈ [ ≈1,6 ; ≈9,4 ] * * *
следовательно:
x ∈ [ 3 ; (11+√61) / 2 ] .
ответ: x ∈ [ 3 ; (11+√61) / 2 ] .
---------------------
3√ ( |x+1| - 3) ≥ √ (x² - 2x - 3)
----------------------------------------
ОДЗ : { |x+1| - 3 ≥ 0 , x² -2x - 3 ≥ 0 .⇔ { |x+1| ≥ 3 , (x+1)(x-3) ≥ 0 . ⇔
|x+1| ≥ 3 ⇔ [ x+1 ≤ - 3 , x+1 ≥ 3 ⇔ [ x ≤ - 4 , x ≥ 2 .
и
(x+1)(x - 3) ≥ 0 ⇔ [ x ≤ - 1 , x ≥ 3.
/////////////////////////////// [ - 4 ] ------------------[2] ////////////////////////////////////////
///////////////////////////////////////////////////[ -1] ---------------- [3] ////////////////////////
x ∈( - ∞ ; - 4 ] ∪ [ 3 ; ∞).
-------------------------------
9|x+1| - 27 ≥ x² -2x - 3 ;
x² - 2x - 9|x+1| + 24 ≤ 0 ;
-------
a)
x ∈ ( - ∞ ; - 4 ]
x² - 2x + 9(x+1) + 24 ≤ 0
x² +7x + 33 ≤ 0 ⇔(x+3,5)² +20,75 ≤ 0 ⇒ x ∈ ∅ .
-------
б)
x ∈ [ 3 ; ∞)
x² - 2x - 9(x+1) + 24 ≤ 0 ;
x² -11x + 15 ≤ 0 ; * * * x₁= (11- √61)/2 , x₂ =(11+√61) / 2 * * *
x ∈ [ (11- √61)/2 ; (11+√61) / 2 ] * * * x ∈ [ ≈1,6 ; ≈9,4 ] * * *
следовательно:
x ∈ [ 3 ; (11+√61) / 2 ] .
ответ: x ∈ [ 3 ; (11+√61) / 2 ] .
Похожие вопросы
Предмет: Информатика,
автор: raz1hsapf1r11
Предмет: Информатика,
автор: rotornay87oxiiuw
Предмет: Физика,
автор: dgrandmother54
Предмет: Алгебра,
автор: Pingvin81