Предмет: Геометрия,
автор: 1717ki5vladavsp1y6ly
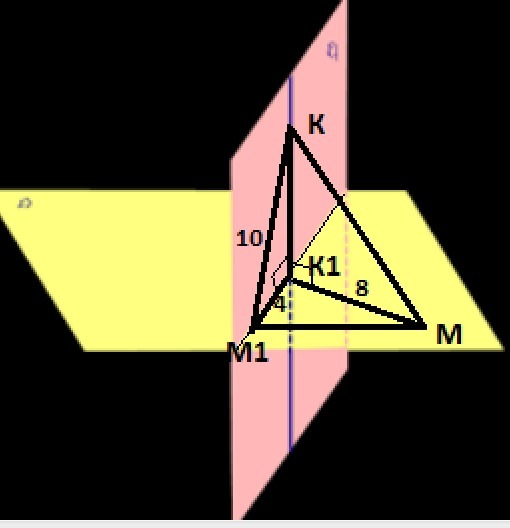
Из точек К и М, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры КК1 и ММ1 на прямую пересечения плоскостей. Найти длину отрезка КМ, если КМ1 = 10. MK1 = 8, M1К1 = 4.
Ответы
Автор ответа:
0
КК1⊥МК, поэтому из т. Пифагора:
КК1=√(М1К²-М1К1²)=√(100-16)=√84
КК1⊥К1М, как прямые, лежащие в перпендикулярных плоскостях, поэтому:
КМ=√(КК1²+ К1М²)=√(84+64)=2√37.
Можно сначала посчитать
катет М1М=√(8²-4²)=√48, затем
КМ=√(100+48)=√148=2√37
КК1=√(М1К²-М1К1²)=√(100-16)=√84
КК1⊥К1М, как прямые, лежащие в перпендикулярных плоскостях, поэтому:
КМ=√(КК1²+ К1М²)=√(84+64)=2√37.
Можно сначала посчитать
катет М1М=√(8²-4²)=√48, затем
КМ=√(100+48)=√148=2√37
Приложения:
Похожие вопросы
Предмет: Физика,
автор: jfgk2djcs8
Предмет: Английский язык,
автор: trumli
Предмет: Биология,
автор: fytazi6
Предмет: Обществознание,
автор: Maggen
Предмет: Алгебра,
автор: pelmen5