Предмет: Алгебра,
автор: igorf5
Помогите решить логарифмическое уравнение
Приложения:
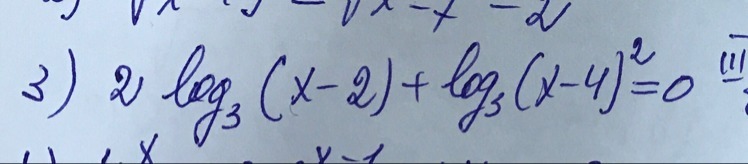
Ответы
Автор ответа:
0
2log₃(x-2)+log₃(x-4)²=0
D(y): x-2>0, x>2
(x-4)²>0, x≠4
x∈(2;4)U(4;+∞)
2log₃(x-2)+2log₃|x-4|=0/:2, x≠4
log₃(x-2)|x-4|=0
log₃(x-2)|x-4|=log₃1
(x-2)|x-4|=1
1) x-4≥0, x≥4, учитывая D(y) → x>4
(x-2)(x-4)=1
x²-4x-2x+8=1
x²-6x+7=0
D=(-6)²-4*1*7=36-28=8
√D=√(4*2)=2√2
x1=(6+2√2)/2=3+√2
x2=(6-2√2)/2=3-√2 - пост. корень
2) x-4<0, x<4, учитывая D(y) → x∈(2;4)
(x-2)(4-x)=1
(x-2)(x-4)=-1
x²-4x-2x+8=-1
x²-6x+9=0
x²-2*x*3+3²=0
(x-3)²=0
x=3
Ответ: x=3, x=3+√2
D(y): x-2>0, x>2
(x-4)²>0, x≠4
x∈(2;4)U(4;+∞)
2log₃(x-2)+2log₃|x-4|=0/:2, x≠4
log₃(x-2)|x-4|=0
log₃(x-2)|x-4|=log₃1
(x-2)|x-4|=1
1) x-4≥0, x≥4, учитывая D(y) → x>4
(x-2)(x-4)=1
x²-4x-2x+8=1
x²-6x+7=0
D=(-6)²-4*1*7=36-28=8
√D=√(4*2)=2√2
x1=(6+2√2)/2=3+√2
x2=(6-2√2)/2=3-√2 - пост. корень
2) x-4<0, x<4, учитывая D(y) → x∈(2;4)
(x-2)(4-x)=1
(x-2)(x-4)=-1
x²-4x-2x+8=-1
x²-6x+9=0
x²-2*x*3+3²=0
(x-3)²=0
x=3
Ответ: x=3, x=3+√2
Автор ответа:
0
ОДЗ
{x-2>0⇒x>2
x-4≠0⇒x≠4
x∈(2;4) U (4;∞)
log_3(x-2)²+log_3(x-4)²=0
log_3[(x-2)(x-4)]²=0
[(x-2)(x-4)]²=1
(x-2)(x-4)=-1 U (x-2)(x-4)=1
x²-6x+9=0 U x²-6x+7=0
(x-3)²=0⇒x-3=0⇒x=3
x²-6x+7=0
D=36-28=8
x1=(6-2√2)/2=3-√2∉ОДЗ
x2=3+√2
Ответ {3;3+√2}
{x-2>0⇒x>2
x-4≠0⇒x≠4
x∈(2;4) U (4;∞)
log_3(x-2)²+log_3(x-4)²=0
log_3[(x-2)(x-4)]²=0
[(x-2)(x-4)]²=1
(x-2)(x-4)=-1 U (x-2)(x-4)=1
x²-6x+9=0 U x²-6x+7=0
(x-3)²=0⇒x-3=0⇒x=3
x²-6x+7=0
D=36-28=8
x1=(6-2√2)/2=3-√2∉ОДЗ
x2=3+√2
Ответ {3;3+√2}
Автор ответа:
0
Почему корень 3-sqrt(2) не удовлетворяет x>2, x(не=4)
Автор ответа:
0
3-1,4=1,6, а ОДЗ x∈(2;4) U (4;∞)
Похожие вопросы
Предмет: Русский язык,
автор: llliissawin
Предмет: Математика,
автор: lnhhv
Предмет: Математика,
автор: darksoul0
Предмет: Химия,
автор: kankulovaa
Предмет: Литература,
автор: Yana04mp