Предмет: Геометрия,
автор: sofiyakuc
Вычислите площадь треугольника, две стороны которого равны 3 см и 2см , а угол между ними 60 градусов. Очень прошу, тк я в 8 классе , не принимайте для решения синусы и т. д.
Ответы
Автор ответа:
0
Дано:
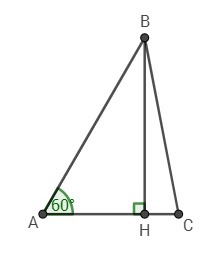
ΔАВС
АВ = 3 см
АС = 2 см
∠А = 60°
Найти: S(ABC)
Опустим высоту ВН. Треугольник АВН - прямоугольный.
∠АВН = 90 - 60 = 30°
Катет, лежащий против угла 30° равен половине гипотенузы, отсюда:
АН = АВ/2 = 3/2
Найдем ВН по теореме Пифагора:

Найдем площадь ΔАВС:
 cм²
cм²
ΔАВС
АВ = 3 см
АС = 2 см
∠А = 60°
Найти: S(ABC)
Опустим высоту ВН. Треугольник АВН - прямоугольный.
∠АВН = 90 - 60 = 30°
Катет, лежащий против угла 30° равен половине гипотенузы, отсюда:
АН = АВ/2 = 3/2
Найдем ВН по теореме Пифагора:
Найдем площадь ΔАВС:
Приложения:
Автор ответа:
0
Спасибо вам большое))
Автор ответа:
0
пожалуйста
Похожие вопросы
Предмет: Химия,
автор: azams3693
Предмет: Физика,
автор: kaydah41
Предмет: Английский язык,
автор: 2006juliaz
Предмет: Музыка,
автор: Secgfgj
Предмет: География,
автор: Аноним