Предмет: Математика,
автор: lizer21
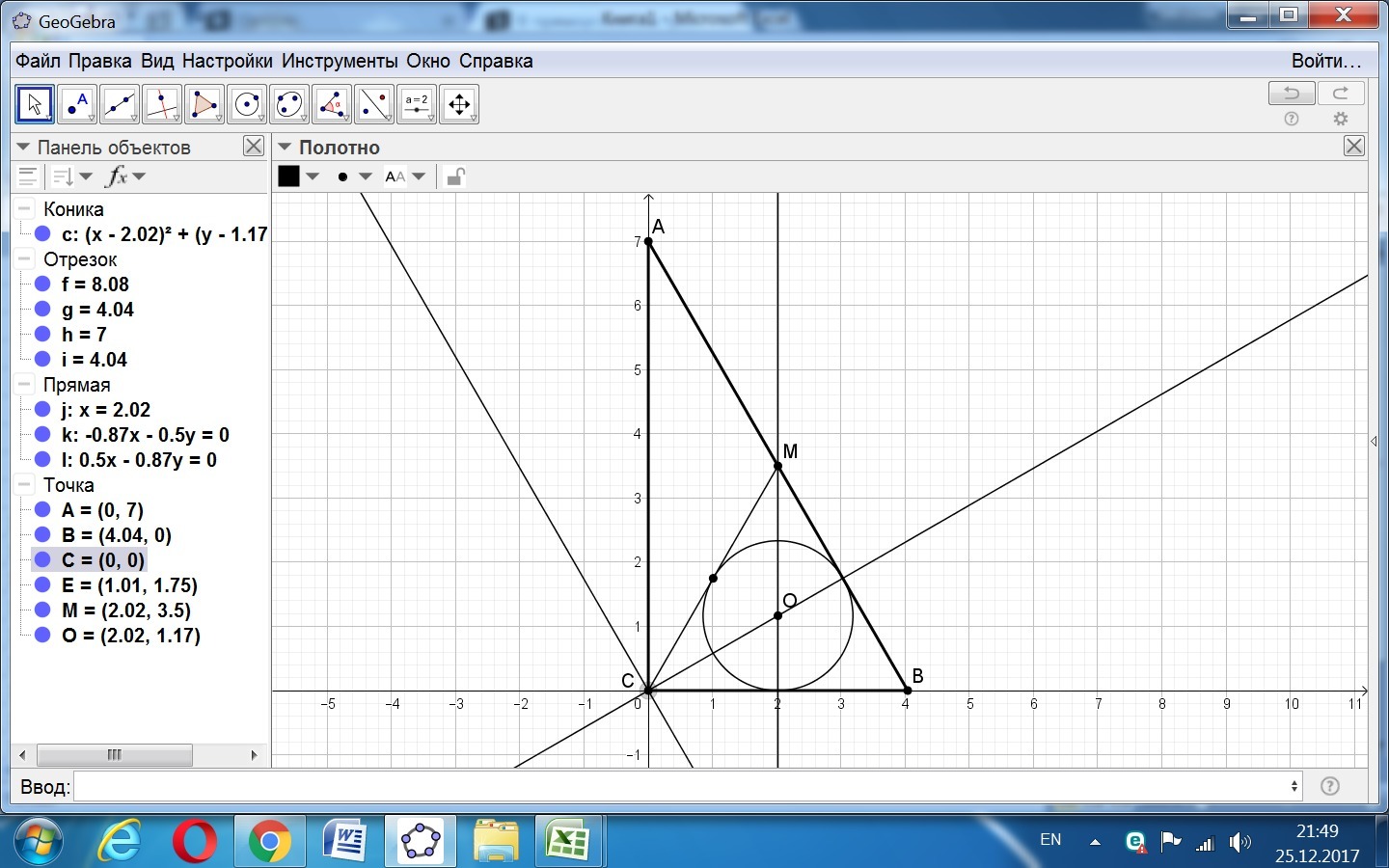
В прямоугольном треугольнике ABC (∠C=90∘) CM - медиана. В треугольник BMC вписана окружность, точка касания делит отрезок BM пополам. Найдите меньший острый угол (в градусах) треугольника ABC.
Ответы
Автор ответа:
0
Имеем прямоугольный треугольник АВС (< C = 90°) и медиану СМ.
В треугольник СМВ вписана окружность так, что СМ делится пополам.
По свойству прямоугольного треугольника СМ равна половине гипотенузы АВ, то есть СМ = МВ.
По свойству касательных и условия, что СМ делится пополам,делаем вывод, что в треугольнике СМВ точки касания делят его стороны на равные отрезки.
То есть треугольник СМВ - равносторонний, острый угос В равен 60 градусов.
Ответ: меньший острый угол равен 90 - 60 = 30 градусов.
В треугольник СМВ вписана окружность так, что СМ делится пополам.
По свойству прямоугольного треугольника СМ равна половине гипотенузы АВ, то есть СМ = МВ.
По свойству касательных и условия, что СМ делится пополам,делаем вывод, что в треугольнике СМВ точки касания делят его стороны на равные отрезки.
То есть треугольник СМВ - равносторонний, острый угос В равен 60 градусов.
Ответ: меньший острый угол равен 90 - 60 = 30 градусов.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: aanaoskonbekova
Предмет: Алгебра,
автор: lizakoksarova693
Предмет: Физика,
автор: razulbekovaa
Предмет: Физика,
автор: VanyaMoshaykin
Предмет: Алгебра,
автор: Kritik1234