Предмет: Математика,
автор: Asemayasdad
y=4x^2-x , y=4-x Вычислите площадь фигуры, ограниченной линиями
Ответы
Автор ответа:
0
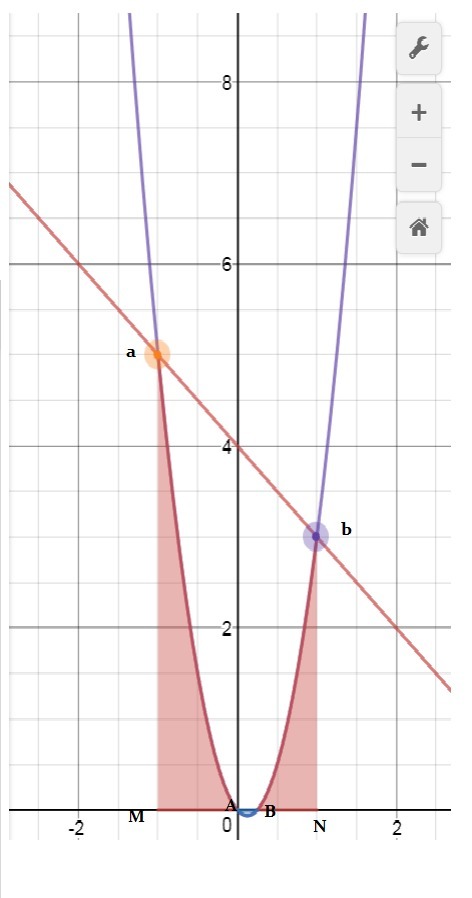
S' - это площадь трапеции.
Найдем a, b и A, B(абсциссы):
a=-1, b=1
A=0, B=0.25;
S'=(3+5)*2/2=8;
Приложения:
Автор ответа:
0
intlimits^{a}_ {b} {f(x)}, dx - это интеграл от a до b функции 4x^2-x по переменной x, далее аналогично. Почему-то не отобразилось(
Похожие вопросы
Предмет: Информатика,
автор: HacKDarK
Предмет: Информатика,
автор: osipovogerlah
Предмет: Қазақ тiлi,
автор: arslanskak64gmailcom
Предмет: Химия,
автор: igot353
Предмет: Математика,
автор: проспоммптр