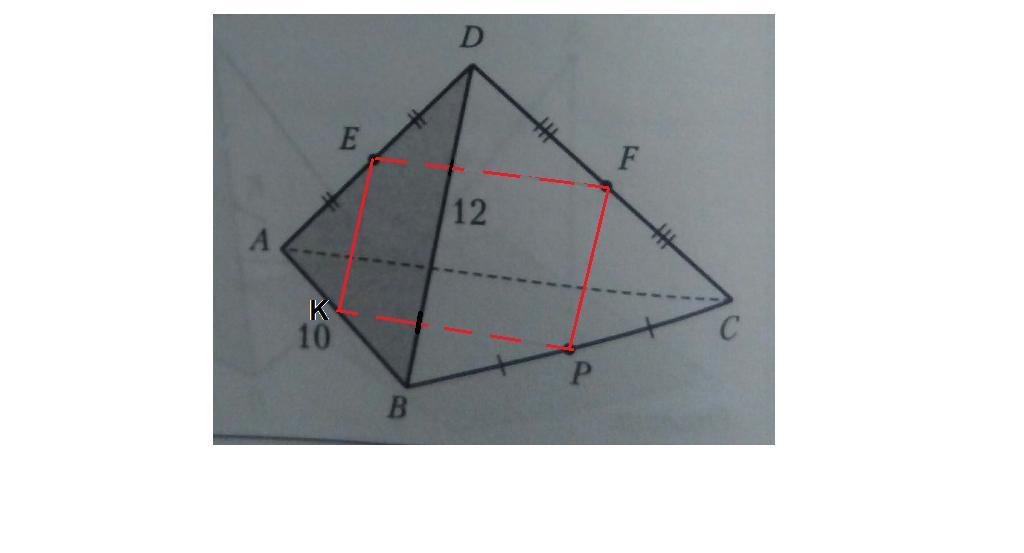
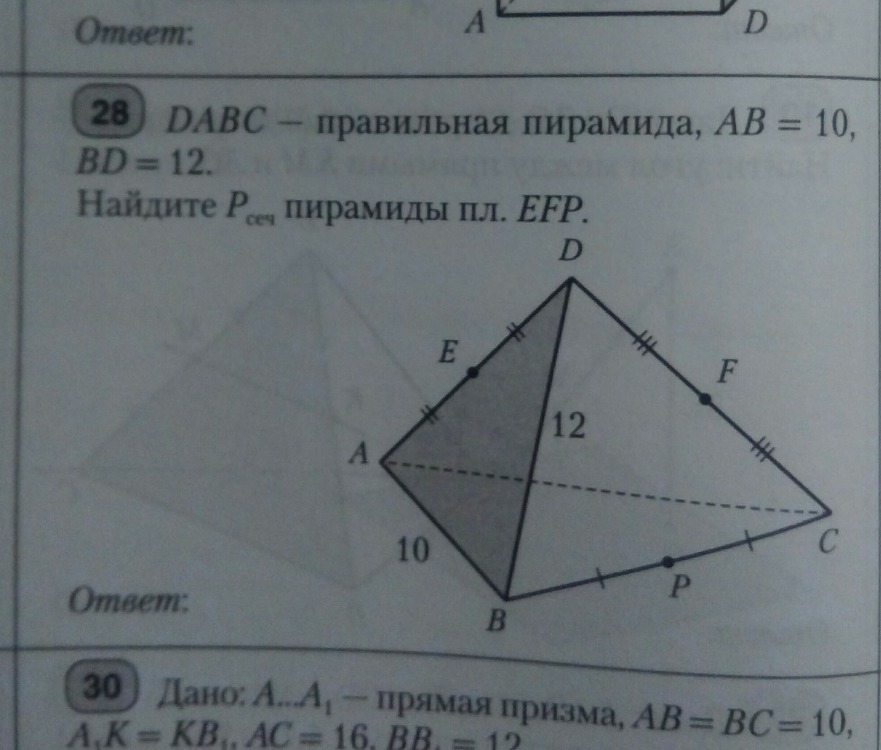
DABC -правильная пирамида AB=10 ,BD=12.
Найдите Рсеч пирамиды пл. ЕFP.
Ответы
Ответ: 22
Объяснение:
Соединим точки F и Е, F и Р, так они попарно лежат в одной грани.
EF - средняя линия треугольника ADC, значит EF║ AC. АС лежит в плоскости АВС, значит EF║(АВС).
Если через прямую, параллельную плоскости, проходит другая плоскость и пересекает первую, то линия пересечения параллельна данной прямой.
Прямая EF параллельна плоскости (АВС), через нее проходит секущая плоскость, значит она пересекает плоскость (АВС) по прямой, параллельной прямой EF.
Тогда проведем РК║АС, а так как АС║EF, то РК║EF.
Соединим точки Е и К.
EFPK - искомое сечение.
Р - середина ВС и РК║АС, значит РК - средняя линия ΔАВС,
РК = 1/2 АС = 5
EF = 1/2 АС = 5 по свойству средней линии треугольника.
FP = 1/2 BD = 6 как средняя линия ΔBDC,
ЕК = 1/2 BD = 6 как средняя линия ΔABD.
Pefpk = EF + FP + PK + EK = 5 + 6 + 5 + 6 = 22