Предмет: Геометрия,
автор: Fortunée
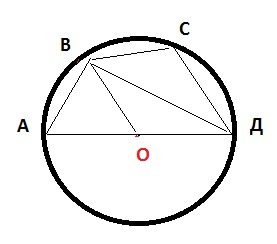
Четырехугольник ABCD вписан в окружность с центром в точке О, принадлежащей стороне AD. BD и AC - диагонали. Найдите градусную меру угла AOB, если извечтны радианные меры углов ADB = п/8 и BDC = п/6.
Ответы
Автор ответа:
0
∠АОВ является центральным, так как О-центр окружности, ∠АДВ-вписанный угол. Вписанный угол= половине центрального угла, опирающегося на ту же дугу. ∠АДВ=1/2∠АОВ
Поэтому ∠АОВ=2∠АДВ
∠АОВ=2∠АДВ=2*π/8=π/4=180/4=45°
Поэтому ∠АОВ=2∠АДВ
∠АОВ=2∠АДВ=2*π/8=π/4=180/4=45°
Приложения:
Похожие вопросы
Предмет: Физкультура и спорт,
автор: 22liza0808
Предмет: Математика,
автор: karinamisina195
Предмет: Алгебра,
автор: marianna25morskaa
Предмет: Математика,
автор: ника498
Предмет: Математика,
автор: eldarermekov