Предмет: Математика,
автор: olesya6789
Помогите решить пожалуйста
Найти частное решение дифференциального уравнения первого порядка, удовлетворяющего начальные условия. y''-4y=0,y(0)=-1,y'=(0)=17/4
Ответы
Автор ответа:
0
Я написал решение на 3х листках...
Приложения:


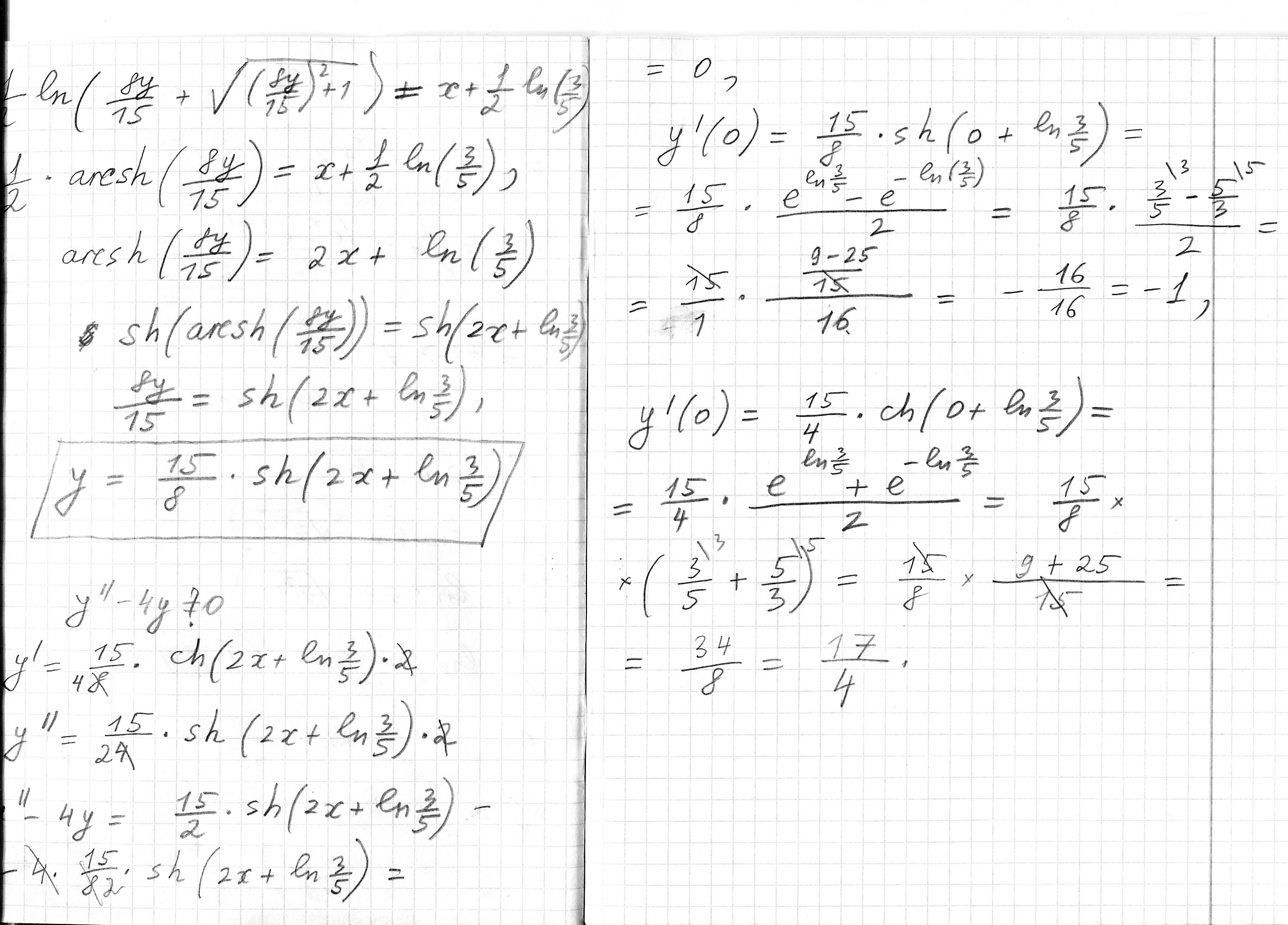
Автор ответа:
0
мы легких путей не ищем! а вообще, упражняться надо.
Автор ответа:
0
Я вас не осуждаю, но владением разных способов - тоже ищем!
Автор ответа:
0
К тому же, ответы у нас должны совпать!
Автор ответа:
0
совпадать!
Автор ответа:
0
а ответы (если присмотреться) совпадают.
Автор ответа:
0
Небольшая поправка. По условию дано именно дифференциальное уравнение второго порядка! Из исходного условия можно понять, что это ДУ второго порядка с постоянными коэффициентами, однородное!!!!
Осуществив замену , получим следующее характеристическое уравнение.
, получим следующее характеристическое уравнение.


Тогда общее решение однородного уравнения примет вид:
 .
.
Осталось найти частное решение, подставив начальные условия

 откуда
откуда 
ЧАСТНОЕ РЕШЕНИЕ:
Осуществив замену
Тогда общее решение однородного уравнения примет вид:
Осталось найти частное решение, подставив начальные условия
ЧАСТНОЕ РЕШЕНИЕ:
Приложения:


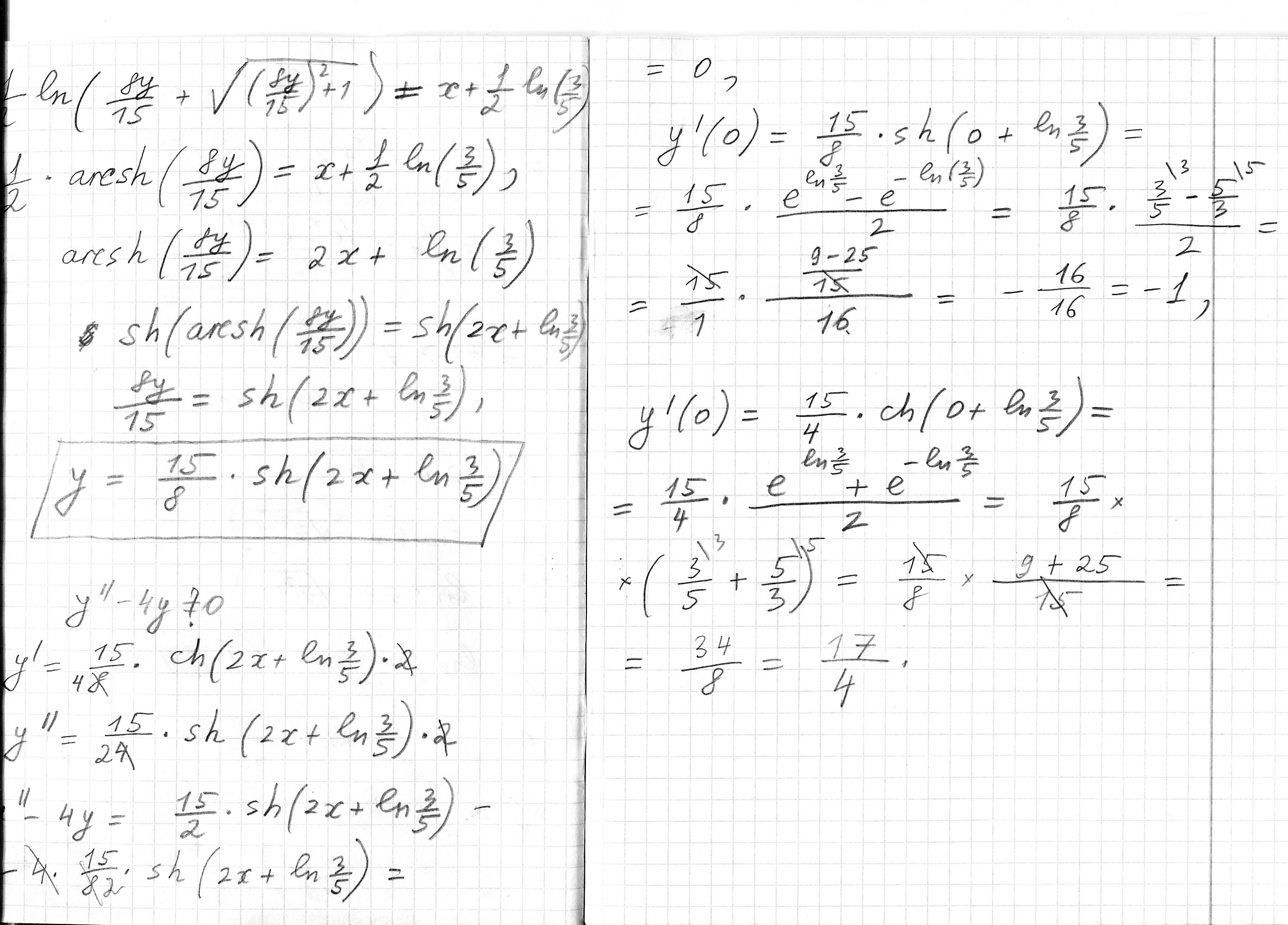
Похожие вопросы
Предмет: Русский язык,
автор: viktorfffgy678
Предмет: Геометрия,
автор: oksanabadaeva41
Предмет: Алгебра,
автор: sherstobitovrustem
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: dolganov1705gmailcom