Question

напишите уравнение к графику функции y=x^3-x+5 в точке X0= -3

Answer 1

ДАНО
y = x³-x+5
НАЙТИ
Касательная в т. Х0 = -3.
РЕШЕНИЕ
Уравнение касательной
F(x) = y'(x)*(x - x0) + y(x0).
Находим производную.
y'(x) = 3*x²-1
Вычисляем при Х0= -3.
y'(-3) = 3*3² - 1 = 27 - 1 = 26.
Вычисляем Y(-3) = -27- (-3)+5) = -19
Уравнение касательной.
F(x) = 26 *(x +3) - 19 = 26*x + 59 - касательная - ОТВЕТ
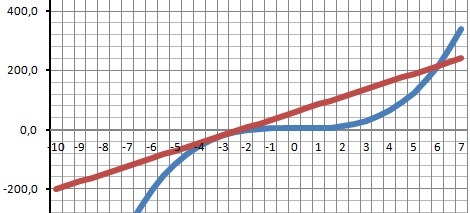
Рисунок с графиком в приложении.