Постройте график функции

Ответы
Раскроем модуль по определению и исследуем получившиеся функции.
Имеем две функции, которые представляют из себя параболы.
Рассмотри сначала ту, что в верхней системе. У неё ветви направлены вверх, вершина параболы:
Найдём её точки пересечения с осями координат:
У нас есть всё чтобы нарисовать эту функцию, далее зачёркиваем весь график, который не удовлетворяет условию: х≥ -0.75
Определим ординату границы:
У параболы второй системы ветви направлены вверх, координата вершины:
Найдём нули функции, находить точки пересечения с осью ординат не имеет смысла т.к. после ограничения часть с этой точкой пропадёт.
Строим параболу по трём точкам (вершина и нули) и отмечаем ограничение х< -0.75, найдём так же ординату границы:
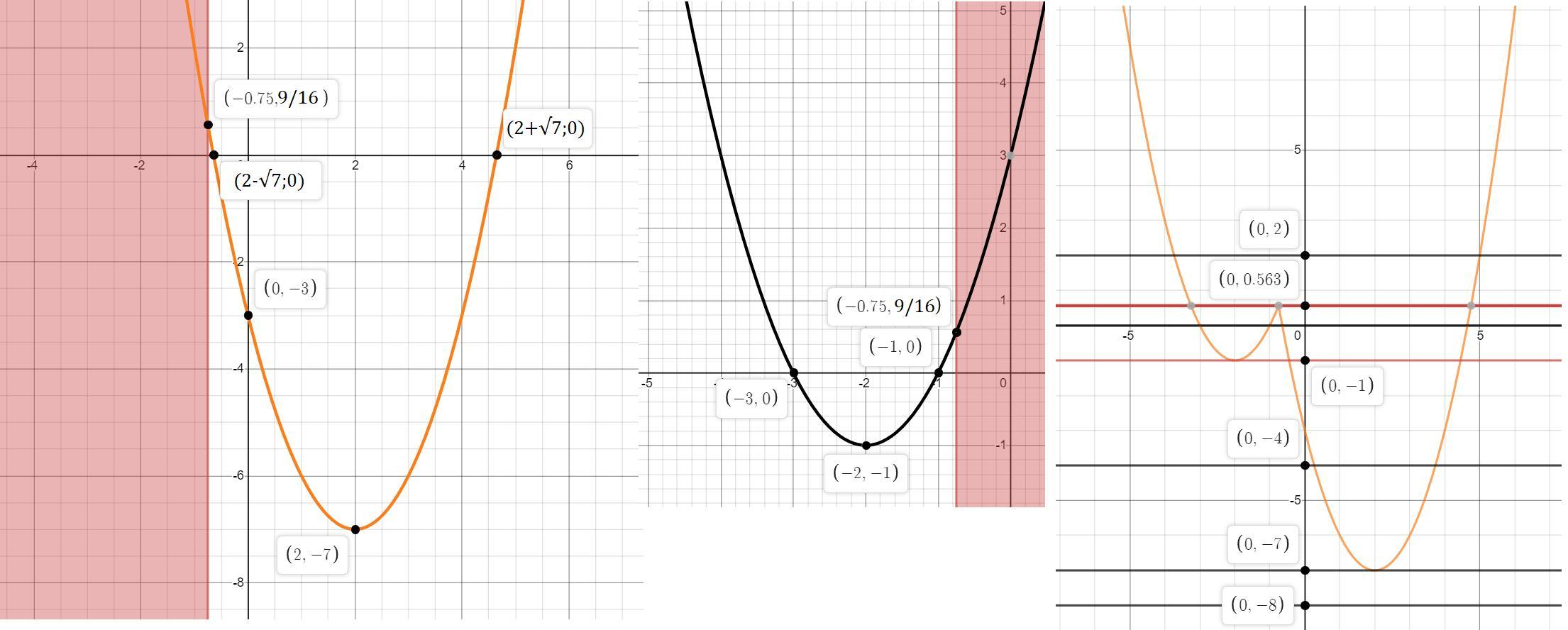
На отдельном графике объединим эти два, как видно точки границ совпадают, значит общая функция получиться непрерывной.
Прямая y=m, параллельно или совпадает с осью Ох, таким образом не сложно догадаться при каких значения параметра m, прямая будет иметь с графиком нашей функции 3 общие точки.
Смотри вниз, чтобы увидеть графики.
m < -7 --> 0 об. точек
m= -7 --> 1 об.т.
-7 < m < -1 --> 2 об.т.
m = -1 --> 3 об.т.
-1 < m < 9/16 --> 2 об.т.
m = 9/16 --> 3 об.т.
m > 9/16 --> 2 об.т.
Нам подходит: m={-1;9/16}
Переведём обыкновенную дробь 9/16 в десятичную:
Ответ: m={-1;0.5625}