Предмет: Алгебра,
автор: Daniil2263
Помогите решить 1.10.15.16.17
Приложения:

Ответы
Автор ответа:
0
Ix+1I+4=0
Ix+1I=-4 решений нет, модуль всегда ≥0
Ix+1I=-4 решений нет, модуль всегда ≥0
Приложения:
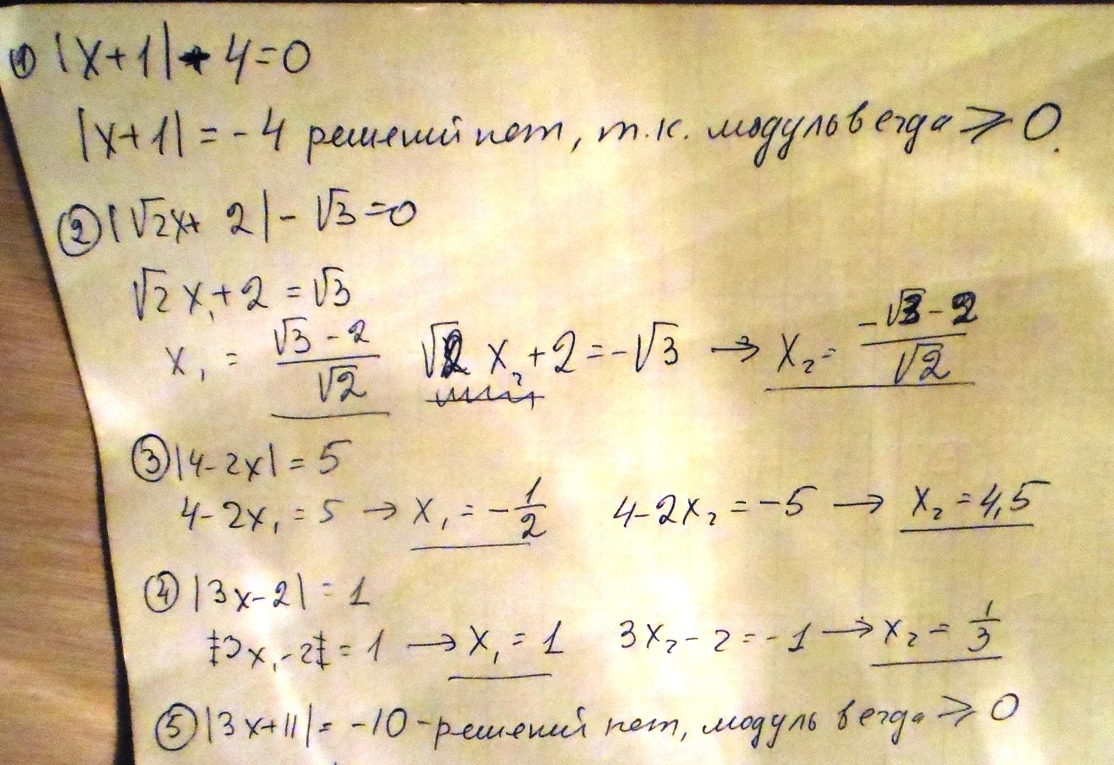
Автор ответа:
0
А можно еще 2.3.5.6?
Автор ответа:
0
Спасибо!!
Автор ответа:
0
обнови страницу, но 6 что-то не получается, несколько раз пробовал. Вроде просто, а начинаю подставлять для проверки - не получается!
Автор ответа:
0
в 6) нет решений...
Автор ответа:
0
1.

нет решений
Ответ: нет решений
2.

нуль подмодульного выражения

значит решения рассматриваем на интервалах

Ответ: x=(-2-√3)/√2 и (√3-2)/√2
3.

нуль подмодульного выражения

значит решения рассматриваем на интервалах

Ответ: x=-1/2 и x=4,5
4.

нуль подмодульного выражения

значит решения рассматриваем на интервалах

5.

нет решений
Ответ: нет решений
6.

Нули подмодульных выражений
 и
и 
 и
и 
значит решения рассматриваем на интервалах

нет решений
![2) x in [1;3] \ 3-x-x+1=4 \ -2x=0 \ x=0 2) x in [1;3] \ 3-x-x+1=4 \ -2x=0 \ x=0](https://tex.z-dn.net/?f=2%29+x+in+%5B1%3B3%5D+%5C+3-x-x%2B1%3D4+%5C+++-2x%3D0+%5C+x%3D0)
не подходит по ОДЗ
нет решений

нет решений
Ответ: нет решений
нет решений
Ответ: нет решений
2.
нуль подмодульного выражения
значит решения рассматриваем на интервалах
Ответ: x=(-2-√3)/√2 и (√3-2)/√2
3.
нуль подмодульного выражения
значит решения рассматриваем на интервалах
Ответ: x=-1/2 и x=4,5
4.
нуль подмодульного выражения
значит решения рассматриваем на интервалах
5.
нет решений
Ответ: нет решений
6.
Нули подмодульных выражений
значит решения рассматриваем на интервалах
нет решений
не подходит по ОДЗ
нет решений
нет решений
Ответ: нет решений
Приложения:
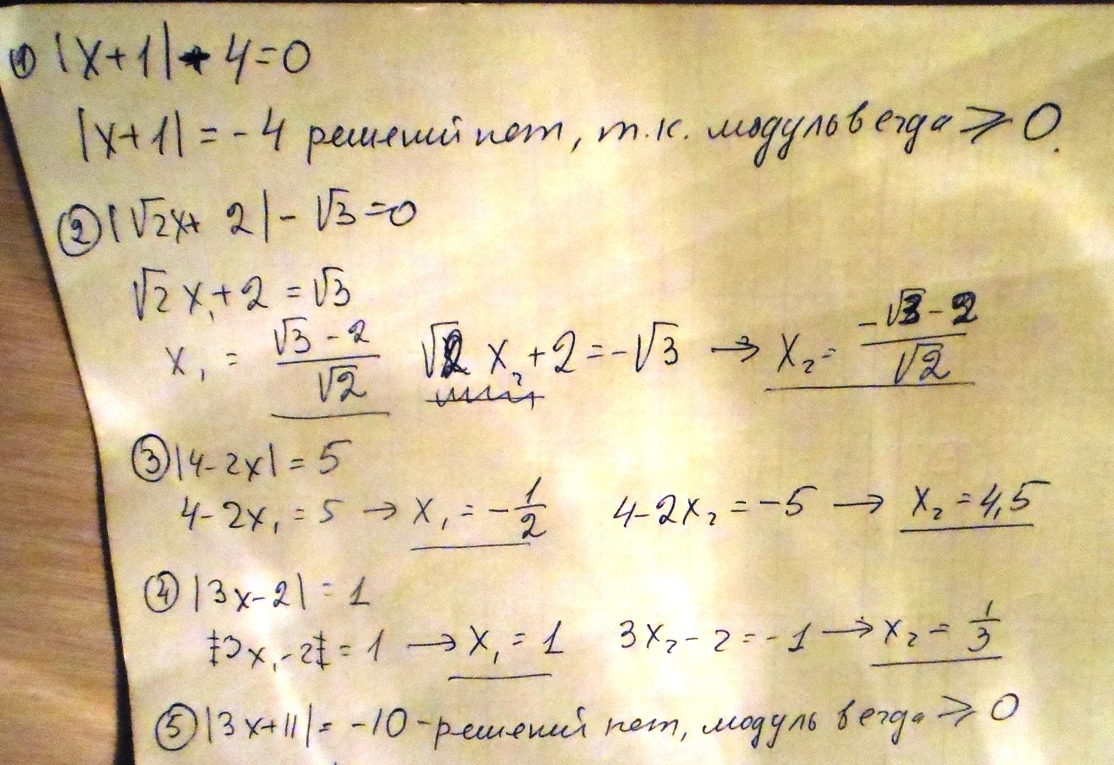
Похожие вопросы
Предмет: География,
автор: ayshaalshan
Предмет: Математика,
автор: valikdemchenko2252
Предмет: Геометрия,
автор: arekamber
Предмет: Биология,
автор: Аноним