Question

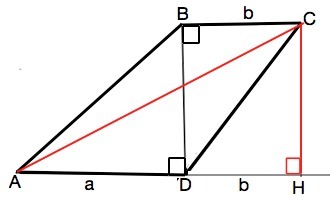
В трапеции ABCD меньшая диагональ BD перпендикулярна основаниям AD и BC, сумма острах углов A и C равно 90 градусов. Найдите длину большей диагонали трапеции, если основание AD=a, BC=b

Answer 1

Треугольники АВD и  СВD  прямоугольные. 

Сумма острых углов прямоугольного треугольника 90°

∠ВАD+∠ABD=90°

∠ВАD+∠ВСD=90° по условию ⇒

∠АВD=∠BCD. 

Если в прямоугольных треугольниках равен один из острых углов. эти треугольники подобны. 

∆ АВD~∆ CBD ⇒ 

BC:BD=BD:AD⇒

BD² =AD•BC=a•b

Опустим из С перпендикуляр до пересечения с продолжением АD в точке Н. 

СН=ВD

СН²=BD²=ab

Из ∆ АСН по т.Пифагора 

АС²=АН²+СН²

АС²=(а+b)²+ab

AC²=a²+2ab+b²+ab=a²+3ab+b²

AC=√(a²+3ab+b²)