Предмет: Математика,
автор: Artem2282283
Найти производную у'
Приложения:
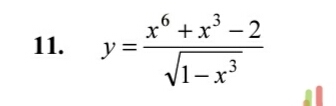


Ответы
Автор ответа:
0
3) прологарифмируем обе части:
Похожие вопросы
Предмет: Информатика,
автор: lzaplavneva
Предмет: Английский язык,
автор: pungaelizaveta
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: КИРиЛл1902
Предмет: География,
автор: Живагина