Предмет: Математика,
автор: Аноним
упростить выражение алгебры множеств
Приложения:
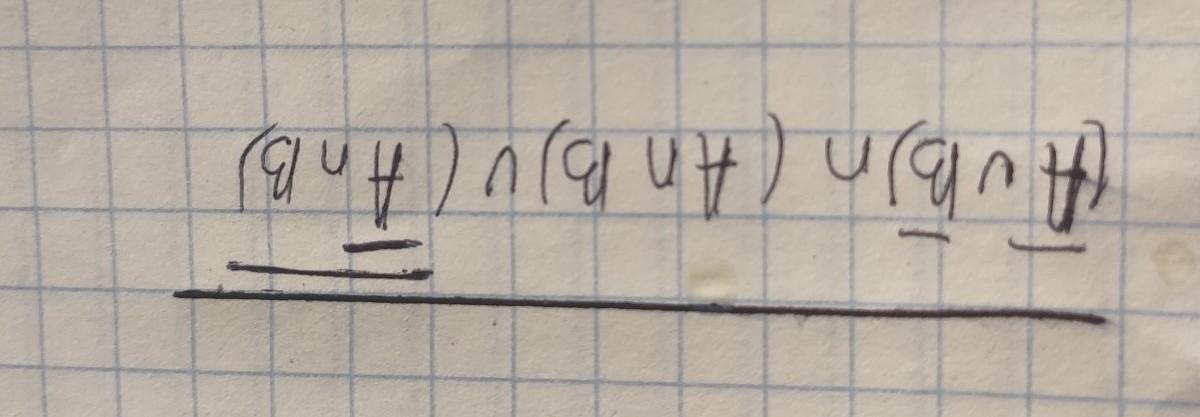
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Смотри рисунок.
1.
2. Используем дистрибутивный закон:
3. Используем ассоциативный закон:
4.
5.
6.
.....
Приложения:
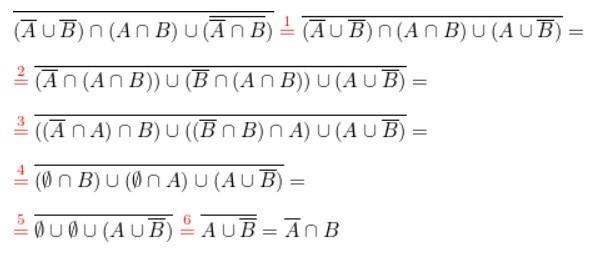
Похожие вопросы
Предмет: Русский язык,
автор: Konowalowjeny
Предмет: Русский язык,
автор: зайк12
Предмет: Математика,
автор: Мимишка1111
Предмет: Математика,
автор: натаван2