Предмет: Геометрия,
автор: verunyaklass
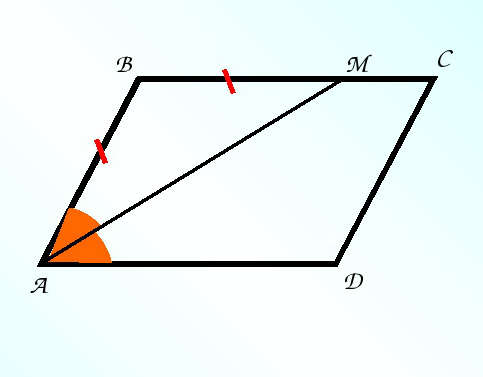
Дан параллелограмм смотрите картинку, надо доказать, что AM биссектриса угла А.
Приложения:
Ответы
Автор ответа:
0
Треугольник АВМ равнобедренный, следовательно в нём угол ВМА равен углу ВАМ. Угол ВМА равен углу МАД (накрестлежащие при параллельных прямых ВС и АД и секущей АМ) => угол ВАМ = углу МАД, а значит АМ биссектриса угла А. Что и требовалось доказать.
Автор ответа:
0
на рисунке у тебя показано что биссектриса ∠ А отсекает равнобедренный треугольник АВМ и делит ∠A пополам.
А по свойствам параллелограмма биссектриса отсекает от параллелограмма равнобедренный треугольник
Если что-то не понятно пиши объясню.
А по свойствам параллелограмма биссектриса отсекает от параллелограмма равнобедренный треугольник
Если что-то не понятно пиши объясню.
Похожие вопросы
Предмет: Математика,
автор: pa3arh00
Предмет: Математика,
автор: IKATEWOW
Предмет: Математика,
автор: chernihln
Предмет: Математика,
автор: podolsckaiapol
Предмет: Экономика,
автор: 4ffhh