Предмет: Математика,
автор: ddaet
Найти точку, симметричную точке A относительно прямой l
Приложения:
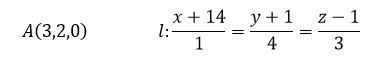
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Уравнение плоскости, перпендикулярной прямой:
(A;B;C) - направляющий вектор. - координаты точки А
Подставим
Прямую l представим в параметрической форме
Найдем точки пересечения прямой и плоскости (в параметрической форме уже выражены через x,y,z, тогда поставляем в )
Координаты точки пересечения:
Известная точка А и искомая точка А', лежат на этой прямой, симметрично точке пересечения двух прямых A₀ (эта точка делит отрезок AA' пополам). Координаты центра отрезка точки A₀ :
— искомая точка
Похожие вопросы
Предмет: Алгебра,
автор: rufinatairova3
Предмет: Русский язык,
автор: egorspakov1
Предмет: Алгебра,
автор: deimonarn
Предмет: Математика,
автор: 55555164