Предмет: Геометрия,
автор: Robin1111
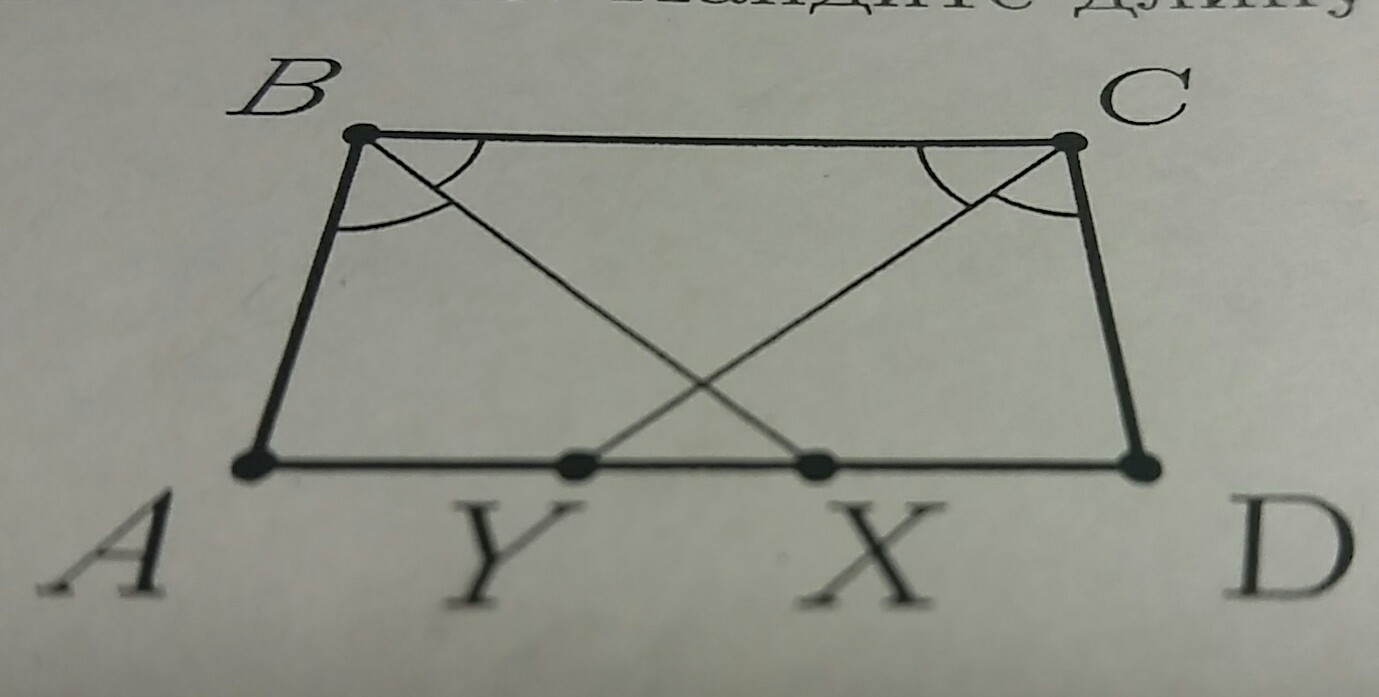
В прямоугольнике ABCD сторона AB равна 6 , сторона BC равна 11 . Из вершин B и C проведены биссектрисы углов , пересекающие сторону AD в точках X и Y соответственно . Найдите длину отрезка XY .
Приложения:
Ответы
Автор ответа:
0
Ответ: 1 (ед. длины)
Объяснение:
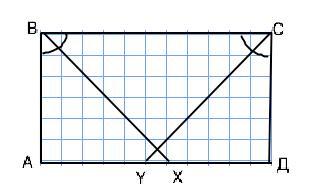
Биссектриса любого угла параллелограмма отсекает от него равнобедренный треугольник, т.к. она делит угол на два равных, один из которых равен накрестлежащему при другом основании (см. рисунок). Поэтому углы ∆ ABX при ВХ равны, углы ∆ CYД при CY равны => ∆ АВХ и ∆ СДY - равнобедренные. АХ=АВ=6, и ДY=СД=6; => ХД=АД-АХ=11-6=5 и AY=АД-ДY=11-6=5. YX=АД-(ХД+АY)=11-10=1
Приложения:
Похожие вопросы
Предмет: Литература,
автор: matur210384
Предмет: Английский язык,
автор: kleserstalker76
Предмет: Русский язык,
автор: volodin54
Предмет: Геометрия,
автор: данилка20021