Question

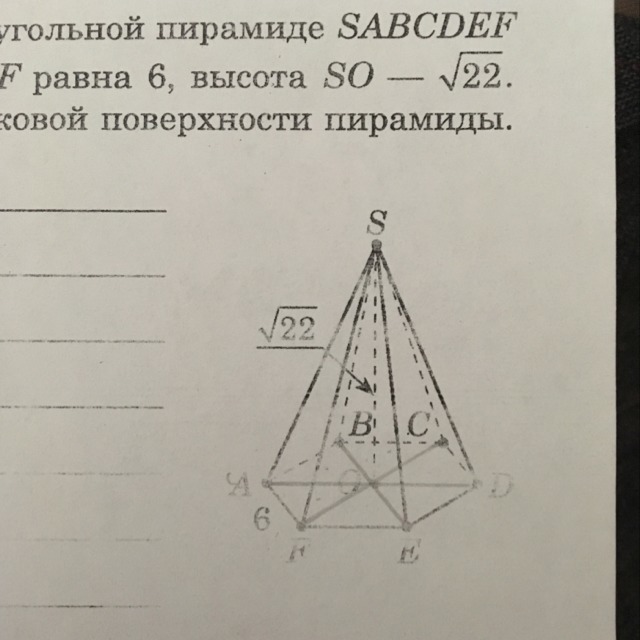
В правильной шестиугольной пирамиде SABCDEF сторона основания AF равна 6, высота SO равна √22. Найдите площадь боковой поверхности пирамиды

Answer 1

Мы знаем, что радиус описанной окружности вокруг правильного шестиугольника равен стороне.
AO=6. SO-высота
По т Пифагора найдем ребро
AS=$sqrt{22+36}= sqrt{58}$
Опустим Апофему из S на сторону AF. треугольник равнобедренный, значит высота - медианта и биссектриса по т Пифагора высота равна 7.
Площадь боковой поверхности равна S=6S1=6*1/2*7*6=126 (т.к шесть равнобедренных треугольников)