Question

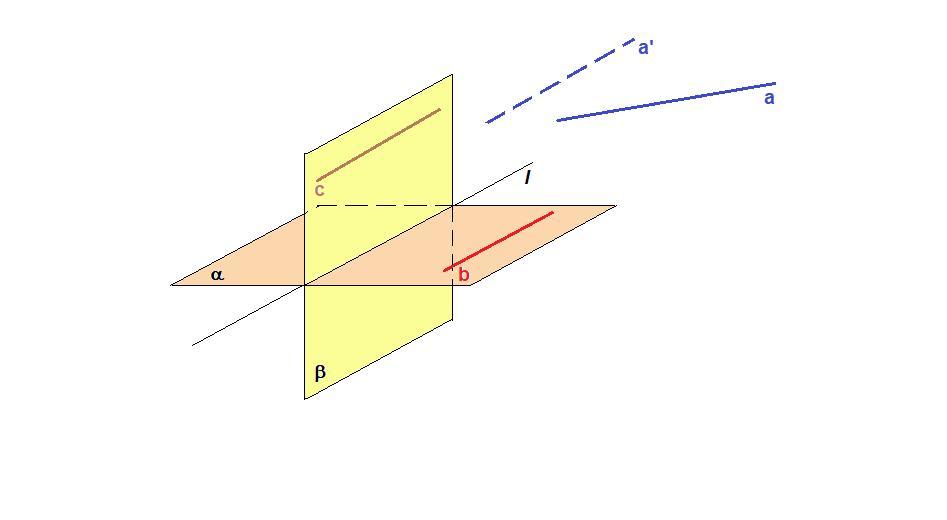
Плоскости альфа и бета пересекаются по прямой l, которой является скрещивающиеся с прямой а. Докажите, что а пересекает хотя бы одну из плоскостей альфа и бета.

Answer 1

Ответ:

Предположим, что прямая а не пересекает плоскости α и β.

Значит, прямая а параллельна обеим плоскостям.

Тогда в каждой плоскости найдется прямая, параллельная прямой а. Пусть это прямые b и с.

Так как b║a и с║а, то b║c.

Если прямая с параллельна прямой b, лежащей в плоскости α, то с║α.

Плоскость β проходит через прямую с, параллельную плоскости α, и пересекает плоскость α, значит линия пересечения плоскостей параллельна прямой с.

Итак, c║l, c║a, ⇒ l║a. Но прямые l и а скрещивающиеся. Получили противоречие.

Значит, прямая а пересекает хотя бы одну из плоскостей.