Предмет: Алгебра,
автор: olegbaldezh
Решите методом алгебраического сложения систему уравнений
Приложения:
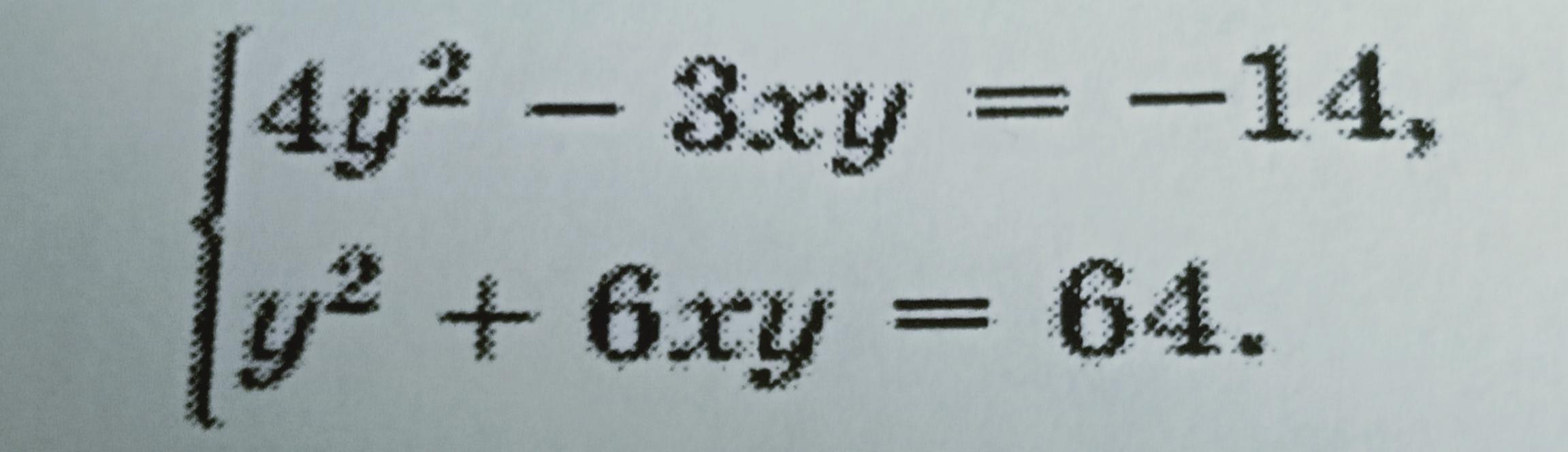
Ответы
Автор ответа:
0
Ответ:
(х₁= 5; у₁= 2); (х₂= -5; у₂= -2)
Объяснение:
умножим первое уравнение на 2
сложим оба уравнения
---------------------
для обоих значений у найдем соответствующие значения х
1)
2)
Ответ: (х₁= 5; у₁= 2); (х₂= -5; у₂= -2)
Похожие вопросы
Предмет: Химия,
автор: DariaPastuhova
Предмет: Литература,
автор: vladgerevicg
Предмет: Физика,
автор: Lera0231
Предмет: Английский язык,
автор: Vkook95971
Предмет: Математика,
автор: Настя57311554454