Предмет: Алгебра,
автор: Розалита12
Как получить из формулы это?
Приложения:
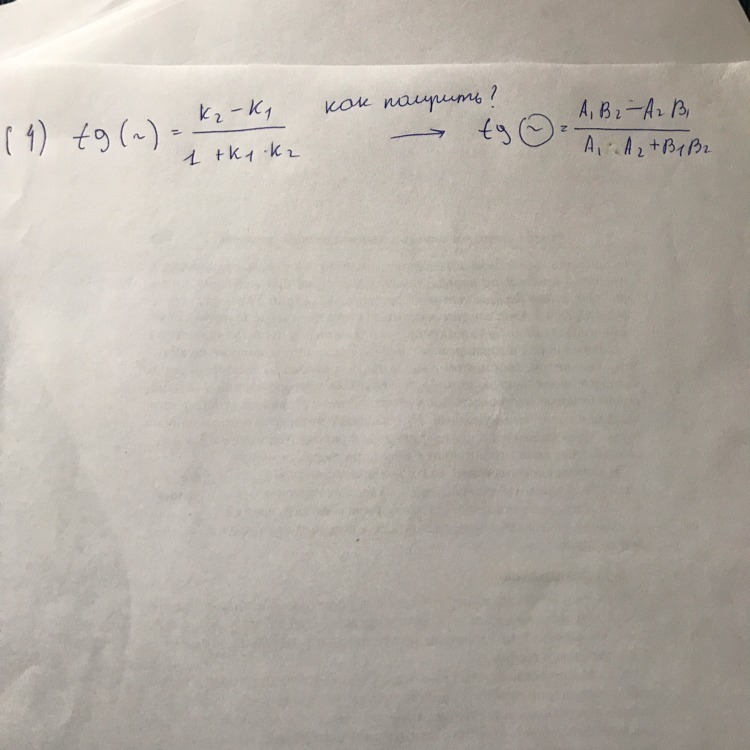
Ответы
Автор ответа:
0
tgα - это угол между двумя прямыми.
В первой формуле эти прямые заданы уравнениями вида y = kx+b.
y₁ = k₁x+b₁ - это уравнение первой прямой
y₂ = k₂x+b₂ - это уравнение второй прямой
В второй формуле эти прямые заданы уравнениями вида Ах+Вy+С = 0
А₁x+В₁у+С₁ = 0 - это уравнение первой прямой
А₂x+В₂у+С₂ = 0 - это уравнение второй прямой
Уравнения
А₁x+В₁у+С₁ = 0
А₂x+В₂у+С₂ = 0
приведем к виду y =kx+b, для этого решим их относительно у.
1) Сначала решим первое уравнение
А₁x+В₁у+С₁ = 0
В₁у = - А₁х + С₁
у = - (А₁/В₁)х + С₁
Сопоставив с формулой y = k₁x+b₁, получим:
k₁ = -(А₁/В₁)
2) Теперь решим второе уравнение
А₂x+В₂у+С₂ = 0
В₂у = - А₂х + С₂
у = - (А₂/В₂)х + С₂
Сопоставив с формулой y = k₂x+b₂, получим:
k₂ = -(А₂/В₂)
3) И, наконец, в данную в условии формулу подставим вместо k₁ и k₂ их значения.
подставим вместо k₁ и k₂ их значения.



В первой формуле эти прямые заданы уравнениями вида y = kx+b.
y₁ = k₁x+b₁ - это уравнение первой прямой
y₂ = k₂x+b₂ - это уравнение второй прямой
В второй формуле эти прямые заданы уравнениями вида Ах+Вy+С = 0
А₁x+В₁у+С₁ = 0 - это уравнение первой прямой
А₂x+В₂у+С₂ = 0 - это уравнение второй прямой
Уравнения
А₁x+В₁у+С₁ = 0
А₂x+В₂у+С₂ = 0
приведем к виду y =kx+b, для этого решим их относительно у.
1) Сначала решим первое уравнение
А₁x+В₁у+С₁ = 0
В₁у = - А₁х + С₁
у = - (А₁/В₁)х + С₁
Сопоставив с формулой y = k₁x+b₁, получим:
k₁ = -(А₁/В₁)
2) Теперь решим второе уравнение
А₂x+В₂у+С₂ = 0
В₂у = - А₂х + С₂
у = - (А₂/В₂)х + С₂
Сопоставив с формулой y = k₂x+b₂, получим:
k₂ = -(А₂/В₂)
3) И, наконец, в данную в условии формулу
Автор ответа:
0
Спасибо огромное, а как 3 пункт записать. ?)
Автор ответа:
0
Там всё записано подробно, только в самом начале вместо дробной черты знак : деления. Это для того, чтобы не было четырёхэтажной дроби.
Похожие вопросы
Предмет: Русский язык,
автор: svetaogonek
Предмет: Английский язык,
автор: TNP88
Предмет: Химия,
автор: duabekovabibysara
Предмет: Физика,
автор: Anqel1na
Предмет: Математика,
автор: жанна110