Question

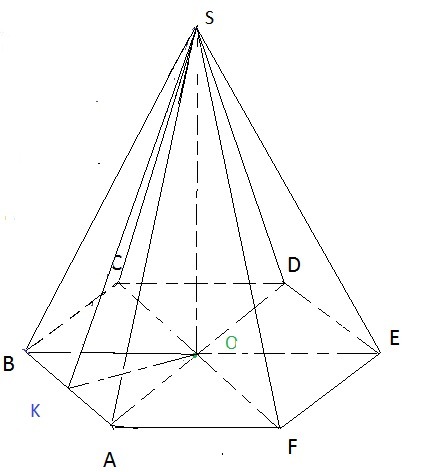
Сторона основания правильной шестиугольной пирамиды 18, боковое ребро 41. Найти площадь боковой поверхности пирамиды

Answer 1

Рассмотрим прямоугольный треугольник SOA в нём радиус описанной окружности основания равен: OA=AB=18. По теореме Пифагора найдем

высоту пирамиды SO.

$SO=sqrt{SA^2-OA^2}=sqrt{41^2-18^2} =sqrt{1357}$

Теперь рассмотрим прямоугольный треугольник SOK. SK - апофема пирамиды, OK - радиус вписанной окружности основания.

OK = AB√3/2 = 9√3

Тогда $SK=sqrt{OK^2+SO^2}=sqrt{(9sqrt{3})^2+(sqrt{1357})^2}= 40$

Площадь одной грани (треугольник SBA): S = AB*SK/2 = 18*40/2 = 360

Площадь боковой поверхности пирамиды- это сумма всех площадей грани . В шестиугольной пирамиде граней 6, значит площадь боковой поверхности пирамиды равна: Sбок = 6*360 = 2160

Ответ: 2160.