Предмет: Алгебра,
автор: LEZENR
Решите уравнение по тригонометрии
Приложения:
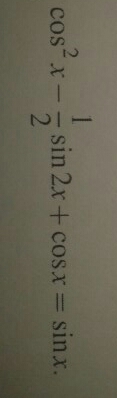
Ответы
Автор ответа:
0
cos²x - 1/2sin2x + cosx = sinx
cos²x - 1/2·2sinxcosx + cosx - sinx = 0
cos²x - sinxcosx + cosx - sinx = 0
cosx(cosx - sinx) + (cosx - sinx) = 0
(cosx + 1)(cosx - sinx) = 0
1) cosx + 1 = 0
cosx = -1
x = π + 2πn, n ∈ Z
2) cosx - sinx = 0
sinx = cosx
tgx = 1
x = π/4 + πk, k ∈ Z
Ответ: x = π + 2πn, n ∈ Z; π/4 + πk, k ∈ Z.
cos²x - 1/2·2sinxcosx + cosx - sinx = 0
cos²x - sinxcosx + cosx - sinx = 0
cosx(cosx - sinx) + (cosx - sinx) = 0
(cosx + 1)(cosx - sinx) = 0
1) cosx + 1 = 0
cosx = -1
x = π + 2πn, n ∈ Z
2) cosx - sinx = 0
sinx = cosx
tgx = 1
x = π/4 + πk, k ∈ Z
Ответ: x = π + 2πn, n ∈ Z; π/4 + πk, k ∈ Z.
Похожие вопросы
Предмет: Русский язык,
автор: renatkulov88
Предмет: Алгебра,
автор: alexandrasid
Предмет: Русский язык,
автор: hadiddailasova
Предмет: История,
автор: смурфа007
Предмет: Алгебра,
автор: Аноним