Предмет: Алгебра,
автор: edinorooog88
Помогите доказать:
(a+b) × (1/a + 1/b) > = 4, если a>0, b>0
Приложения:
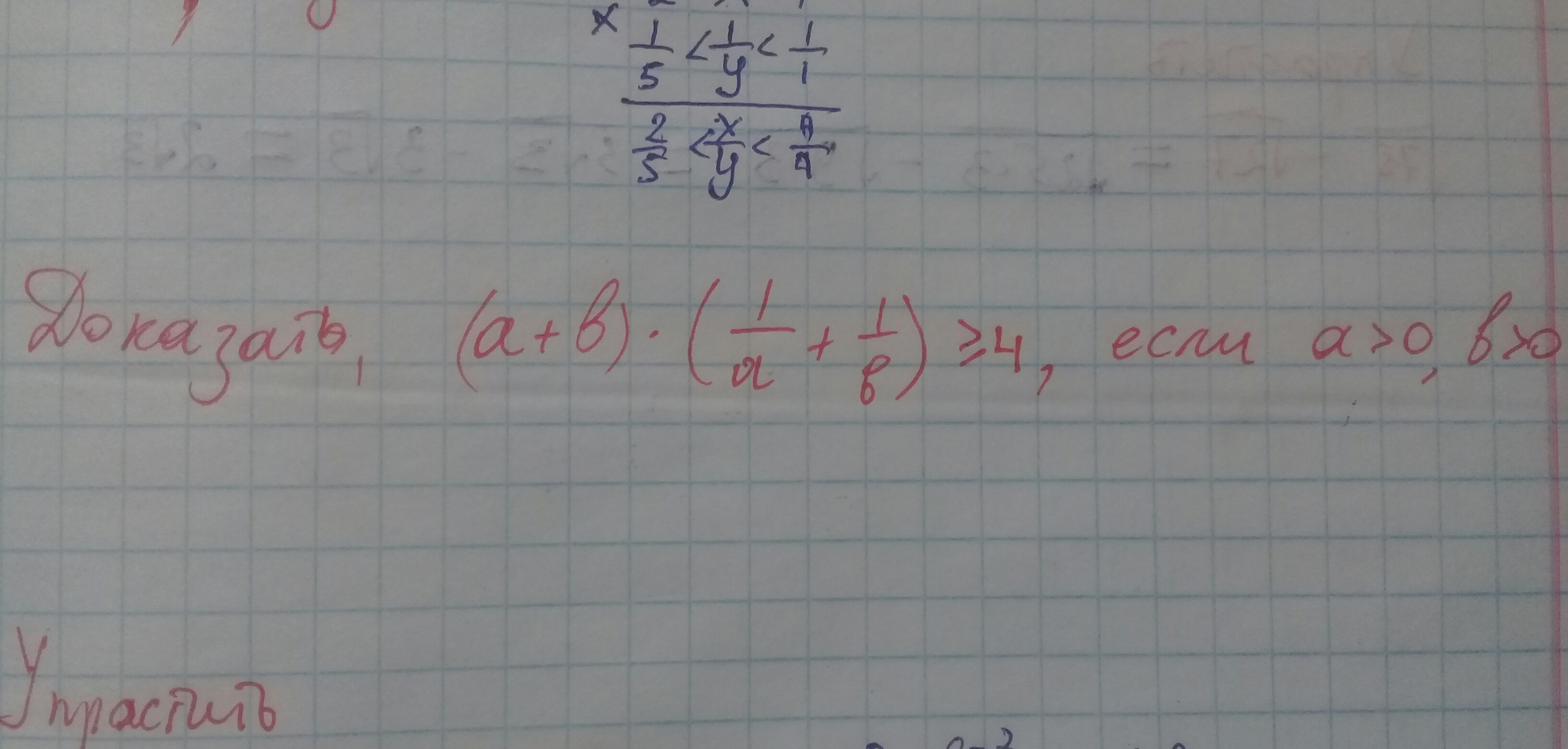
Ответы
Автор ответа:
0
Числитель всегда неотрицателен т.к в квадрате, знаменатель больше нуля, т.к a>0 и b>0
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Право,
автор: moron50
Предмет: Математика,
автор: zuhriddindadazonov91
Предмет: Информатика,
автор: mcgold
Предмет: Алгебра,
автор: villpotter