Предмет: Математика,
автор: Аноним
Решите пожалуйста
с подробным решением с очень подробным и с ответом ,даю 100 баллов
Приложения:
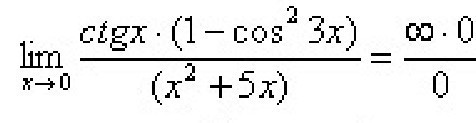
Ответы
Автор ответа:
0
Используем эквивалентные функции (две функции называются эквивалентными, если предел их отношения равен 1. Это записывается так: f ~ g)
ctg x = cos x / sin x ~ 1/x (следствие из первого замечательного предела)
1 - cos^2(3x) = sin^2(3x) ~ (3x)^2 (тоже из первого замечательного предела)
ctg x (1 - cos^2(3x))/(x^2 + 5x) ~ 1/x * 9x^2 / (x (x + 5)) = 9 / (x + 5)

_______________________

Основное тригонометрическое тождество: sin^2(x) + cos^2(x) = 1
Определение ctg x: ctg x = cos x / sin x
Первый замечательный предел: lim sin x / x = 1
ctg x = cos x / sin x ~ 1/x (следствие из первого замечательного предела)
1 - cos^2(3x) = sin^2(3x) ~ (3x)^2 (тоже из первого замечательного предела)
ctg x (1 - cos^2(3x))/(x^2 + 5x) ~ 1/x * 9x^2 / (x (x + 5)) = 9 / (x + 5)
_______________________
Основное тригонометрическое тождество: sin^2(x) + cos^2(x) = 1
Определение ctg x: ctg x = cos x / sin x
Первый замечательный предел: lim sin x / x = 1
Автор ответа:
0
Начиная с какого места в строчке ctg x (1 - cos^2(3x))/(x^2 + 5x) ~ 1/x * 9x^2 / (x (x + 5)) = 9 / (x + 5) становится непонятно?
Похожие вопросы
Предмет: Английский язык,
автор: 23lelik139
Предмет: История,
автор: Аноним
Предмет: История,
автор: evakondrateva579
Предмет: Алгебра,
автор: Аноним