Предмет: Алгебра,
автор: Змей24
Найдите границу: 
Ответы
Автор ответа:
0
Если подставим значение x=0 получим неопределенность вида 0/0.
Очевидно что функции дифференцируемы в любой точке, следовательно они дифференцируемы в окрестности точки x=0. Очевидно что
дифференцируемы в любой точке, следовательно они дифференцируемы в окрестности точки x=0. Очевидно что  .
.
Найдем следующий предел:
 .
.
Следовательно, по правилу Лопиталя:

Очевидно что функции
Найдем следующий предел:
Следовательно, по правилу Лопиталя:
Автор ответа:
0
Воспользуемся замечательным пределом 
Представим выражение в так:

Представим выражение в так:
Приложения:
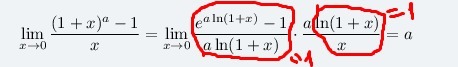
Автор ответа:
0
Это гениально!
Похожие вопросы
Предмет: Алгебра,
автор: rogacevaaleksandra38
Предмет: Геометрия,
автор: pushkinavaleria
Предмет: Математика,
автор: rimodingod
Предмет: Литература,
автор: анна172005
Предмет: Математика,
автор: dandih75