Предмет: Алгебра,
автор: slavaekb
Вычислите кто-нибудь ,не получается
Приложения:
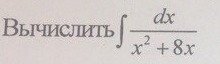
Ответы
Автор ответа:
0
Ну изи же. Дробно рациональные функции.
![\displaystyle
\frac{1}{x^2+8x} = \frac{1}{x(x+8)} = \left[\frac{1}{x}-\frac{1}{x+8}\right]/8\\\\
\int\frac{dx}{x^2+8x} = \int\frac{dx}{8x}-\int\frac{dx}{8(x+8)} = \frac{1}{8}\ln\frac{x}{x+8}+C \displaystyle
\frac{1}{x^2+8x} = \frac{1}{x(x+8)} = \left[\frac{1}{x}-\frac{1}{x+8}\right]/8\\\\
\int\frac{dx}{x^2+8x} = \int\frac{dx}{8x}-\int\frac{dx}{8(x+8)} = \frac{1}{8}\ln\frac{x}{x+8}+C](https://tex.z-dn.net/?f=%5Cdisplaystyle%0A%5Cfrac%7B1%7D%7Bx%5E2%2B8x%7D+%3D+%5Cfrac%7B1%7D%7Bx%28x%2B8%29%7D+%3D+%5Cleft%5B%5Cfrac%7B1%7D%7Bx%7D-%5Cfrac%7B1%7D%7Bx%2B8%7D%5Cright%5D%2F8%5C%5C%5C%5C%0A%5Cint%5Cfrac%7Bdx%7D%7Bx%5E2%2B8x%7D+%3D+%5Cint%5Cfrac%7Bdx%7D%7B8x%7D-%5Cint%5Cfrac%7Bdx%7D%7B8%28x%2B8%29%7D+%3D+%5Cfrac%7B1%7D%7B8%7D%5Cln%5Cfrac%7Bx%7D%7Bx%2B8%7D%2BC)
Автор ответа:
0
x²+8x имеет действительные корни поэтому можем воспользоватся специальным разложением дробей( сори, забыл как называется)
x²+8x=x(x+8) значит имеем интеграл от дроби
 приведем правую часть к общему знаменателю:
приведем правую часть к общему знаменателю:
 , теперь сократим знаменатель получив равенство:
, теперь сократим знаменатель получив равенство:
1=A(x+8)+Bx чтобы найти А и B приравняем коэфициэнты при одинаковых степенях икс. Получим систему уравнений откуда найдем А и В:
 откуда
откуда  и В=
и В= . Теперь перепишем исходный интеграл и найдем его:
. Теперь перепишем исходный интеграл и найдем его:
 =
=  +C
+C
x²+8x=x(x+8) значит имеем интеграл от дроби
1=A(x+8)+Bx чтобы найти А и B приравняем коэфициэнты при одинаковых степенях икс. Получим систему уравнений откуда найдем А и В:
Похожие вопросы
Предмет: Физика,
автор: sqphm
Предмет: Геометрия,
автор: shelenkodasha
Предмет: Математика,
автор: natusazuravskaa
Предмет: Физкультура и спорт,
автор: AlekseyNad
Предмет: Математика,
автор: mahamatjonovanilufar