Предмет: Алгебра,
автор: Rodey
Вычислить Sin a и cos a, если tg a = √(2/7) ; промежуток от 6П до 13\2; Спасибо !
amin07am:
13/2 pi?или без него?
13п/2
Ответы
Автор ответа:
22
Т.к. у функций y = sinx и y = cosx основной период - 2π, то значения на отрезке [6π; 13π/2] будут такие же, как и на отрезке [0; π/2].
На отрезке [0; π/2] и синус, и косинус, и тангенс принимают неотрицательные значения.
Используем формулу, связывающую тангенс и косинус одного угла и основное тригонометрическое тождество:

На отрезке [0; π/2] и синус, и косинус, и тангенс принимают неотрицательные значения.
Используем формулу, связывающую тангенс и косинус одного угла и основное тригонометрическое тождество:
Автор ответа:
4
Решение во вложенном файле
Приложения:
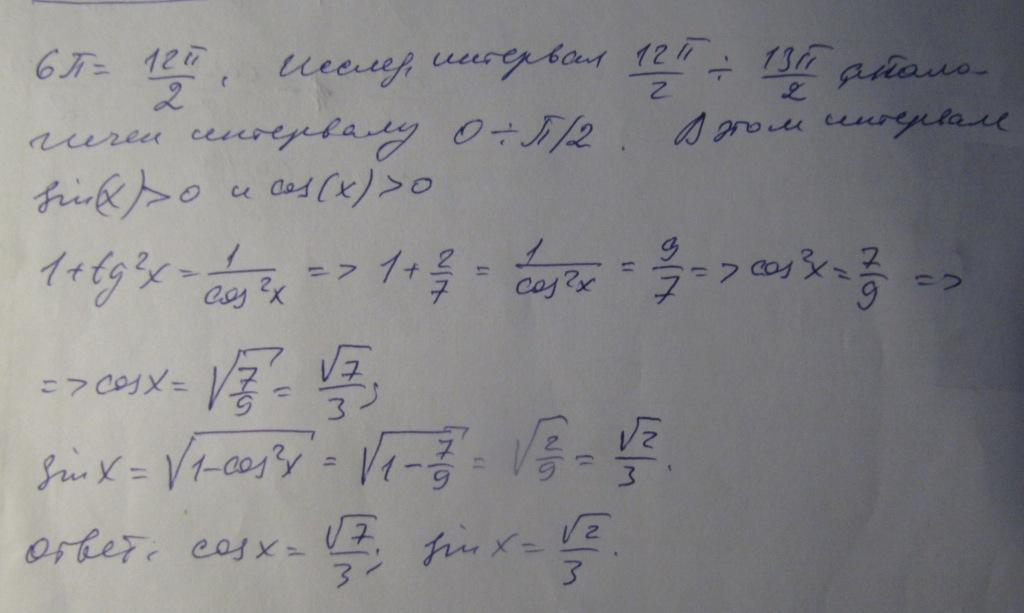
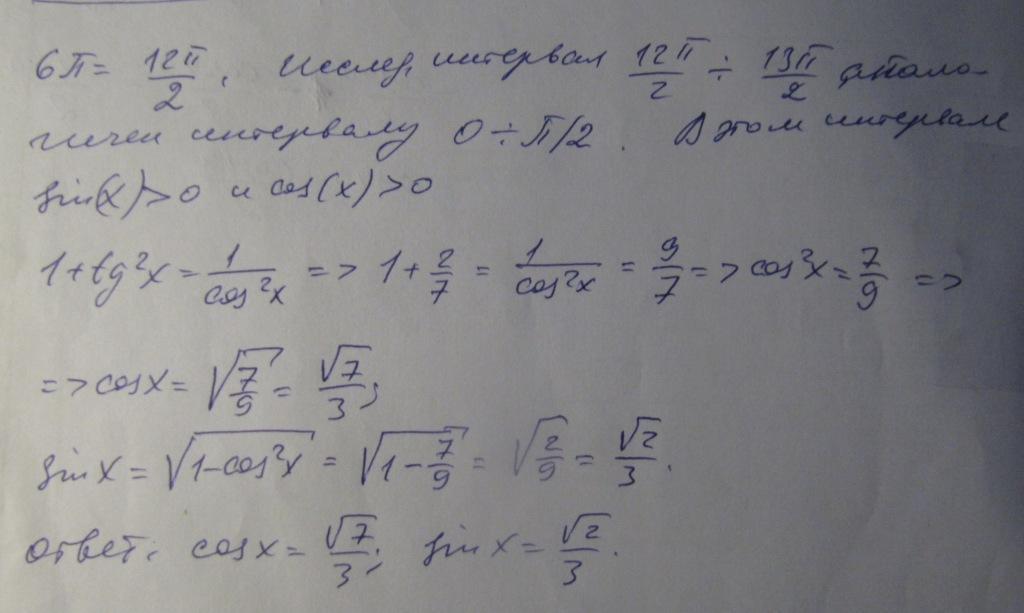
Похожие вопросы
Предмет: Геометрия,
автор: shelenkodasha
Предмет: Математика,
автор: natusazuravskaa
Предмет: Другие предметы,
автор: yuliaredmi8
Предмет: Математика,
автор: mahamatjonovanilufar
Предмет: Математика,
автор: vovazamatin1