Предмет: Алгебра,
автор: АкемиСузуки78
Логарифмическое неравенство - помогите пожалуйста разобраться. Не получается ответ.
Приложения:
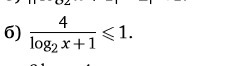
Ответы
Автор ответа:
1
4/(log₂ x+1)≤1
4/(log₂ x+1)-1≤0
(4-log₂ x-1)/(log₂ x+1)≤0
(3-log₂ x)/(log₂ x+1)≤0
log₂x=t одз x>0
(3-t)/(t+1)≤0
------------ (-1) +++++ [3] ------------
получили систему
x>0 x>0
log₂x<-1 x<1/2
log₂x≥3 x≥8
x∈(0 1/2) U [8 +∞)
4/(log₂ x+1)-1≤0
(4-log₂ x-1)/(log₂ x+1)≤0
(3-log₂ x)/(log₂ x+1)≤0
log₂x=t одз x>0
(3-t)/(t+1)≤0
------------ (-1) +++++ [3] ------------
получили систему
x>0 x>0
log₂x<-1 x<1/2
log₂x≥3 x≥8
x∈(0 1/2) U [8 +∞)
Автор ответа:
1
ОДЗ
{x>0
{log(2)x+1≠0⇒log(2)x≠-1⇒x≠1/2
x∈(0;0,5) U (0,5;∞)
4/(log(2)x+1)-1≤0
(4-log(2)x -1)/(log(2x+1)≤0
(3-log(2)x)/(log(2)x+1)≤0
1){3-log(2)x≤0⇒log(2)x≥3⇒x≥8
{log(2)x+1>0⇒log(2)x>-1⇒x>0,5
x≥8
2){3-log(2)x≥0⇒log(2)x≤3⇒x≤8
{log(2)x+1<0⇒log(2)x<-1⇒x<0,5
x<0,5 +ОДЗ⇒0<x<0,5
Ответ x∈(0;0,5) U [8;∞)
{x>0
{log(2)x+1≠0⇒log(2)x≠-1⇒x≠1/2
x∈(0;0,5) U (0,5;∞)
4/(log(2)x+1)-1≤0
(4-log(2)x -1)/(log(2x+1)≤0
(3-log(2)x)/(log(2)x+1)≤0
1){3-log(2)x≤0⇒log(2)x≥3⇒x≥8
{log(2)x+1>0⇒log(2)x>-1⇒x>0,5
x≥8
2){3-log(2)x≥0⇒log(2)x≤3⇒x≤8
{log(2)x+1<0⇒log(2)x<-1⇒x<0,5
x<0,5 +ОДЗ⇒0<x<0,5
Ответ x∈(0;0,5) U [8;∞)
Похожие вопросы
Предмет: Алгебра,
автор: vovaklevec5
Предмет: Английский язык,
автор: cudllies70
Предмет: Химия,
автор: carenkoaroslav
Предмет: Английский язык,
автор: StrangeR213
Предмет: Алгебра,
автор: apoprp282