Предмет: Математика,
автор: dyea
решите пожалуйста...
Приложения:
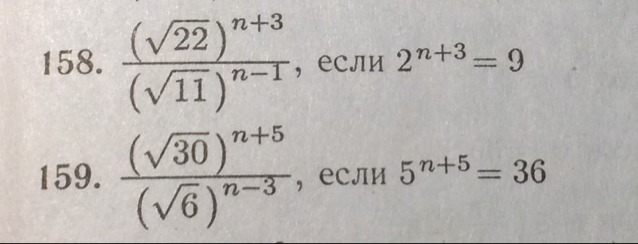
Ответы
Автор ответа:
0
√x = x (в степени (1/2))
при делении степеней с одинаковым основанием, показатели степени вычитаются...
при делении степеней с одинаковым основанием, показатели степени вычитаются...
Приложения:
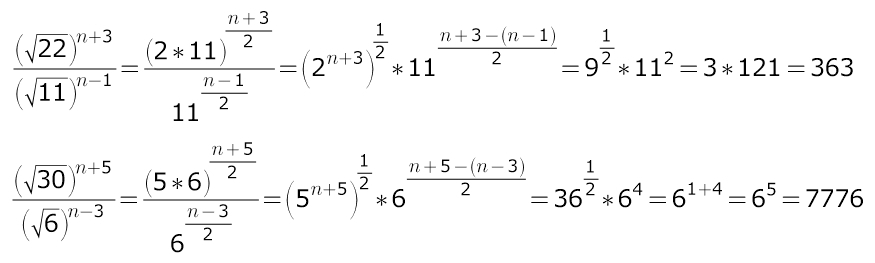
Автор ответа:
0
Степень можно внести под корень, а потом объединить корни числителя и знаменателя.
158.
(√(22))^(n+3) √(22^*(n+3)) (2 * 11)^(n+3) 2^(n+3) * 11^(n+3)
------------------ = ----------------- = √ ------------------- = √--------------------------- =
(√(11))^(n-1) √(11^(n-1)) 11^(n-1) 11^(n-1)
= √(2^(n+3)) * √(11^4) = √9 * 11^2 = 3 * 121 = 363
159. Аналогично.
(√(30))^(n+5) 5^(n+5) * 6^(n+5)
------------------ = √ ------------------------- = √(5^(n+5)) * √(6^8) = √36 * 6^4 =
(√(6)^(n-3) 6^(n-3)
= 6 * 6^4 = 6^5 = 7776
158.
(√(22))^(n+3) √(22^*(n+3)) (2 * 11)^(n+3) 2^(n+3) * 11^(n+3)
------------------ = ----------------- = √ ------------------- = √--------------------------- =
(√(11))^(n-1) √(11^(n-1)) 11^(n-1) 11^(n-1)
= √(2^(n+3)) * √(11^4) = √9 * 11^2 = 3 * 121 = 363
159. Аналогично.
(√(30))^(n+5) 5^(n+5) * 6^(n+5)
------------------ = √ ------------------------- = √(5^(n+5)) * √(6^8) = √36 * 6^4 =
(√(6)^(n-3) 6^(n-3)
= 6 * 6^4 = 6^5 = 7776
Приложения:
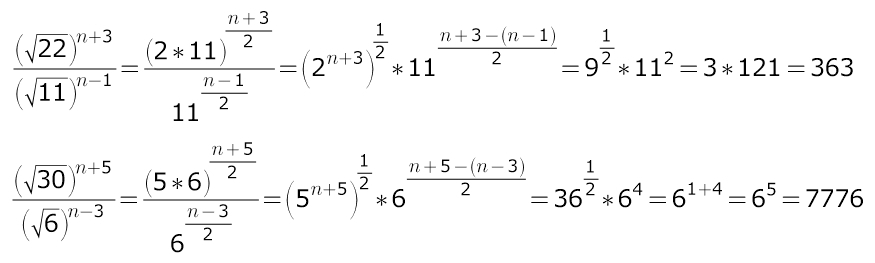
Похожие вопросы
Предмет: Другие предметы,
автор: tanaskrut
Предмет: История,
автор: polinka4614
Предмет: Информатика,
автор: sneyzirose
Предмет: Математика,
автор: Настя13Козов