Предмет: Математика,
автор: mitin7092
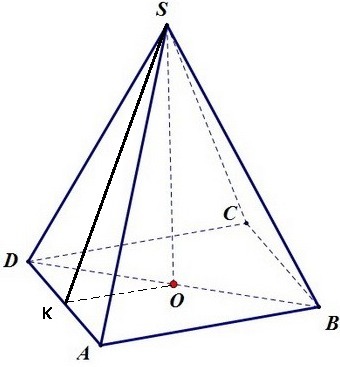
Найдите объем правильной четырехугольной пирамиды, боковое ребро которой равно 5 см, а высота равна 4 см.
Ответы
Автор ответа:
5
По условию SA=SB=SC=SD = 5 см, SO = 4 см.
Объем пирамиды вычисляется по формуле , где So - площадь основания.
, где So - площадь основания.
Вычислим из прямоугольного треугольника
из прямоугольного треугольника  , т.е. по т. Пифагора
, т.е. по т. Пифагора  см. Тогда
см. Тогда  см. Вычислив площадь основания по формуле
см. Вычислив площадь основания по формуле  , получим
, получим  см²
см²
Тогда объем пирамиды см³
см³
Ответ: 24 см³
Объем пирамиды вычисляется по формуле
Вычислим
Тогда объем пирамиды
Ответ: 24 см³
Приложения:
Похожие вопросы
Предмет: Математика,
автор: radmircrmp98
Предмет: Другие предметы,
автор: andreiskyratovich301
Предмет: Английский язык,
автор: tarasorisyk
Предмет: Другие предметы,
автор: SRALIN
Предмет: Литература,
автор: annsavchuk08