Предмет: Алгебра,
автор: iEsse
Помогите найти вершину параболы y=3x-x^3
Dимасuk:
Степень точно кубическая? А не квадратная
Да, но там можно вынести x и получится x(3-x^2)
ну так вершины не будет
будут точки экстремума
У меня в задаче просят найти площадь фигуры ограниченной графиком y=3x-x^3 и прямыми x=0 x=1 y=0, для этого нужно построить параболу, а мне не очень понятно что куда подставить в формул -b/2a
Да и как у параболы не может быть вершины
Определённый интеграл можно и без графика посчитать
Ответы
Автор ответа:
0
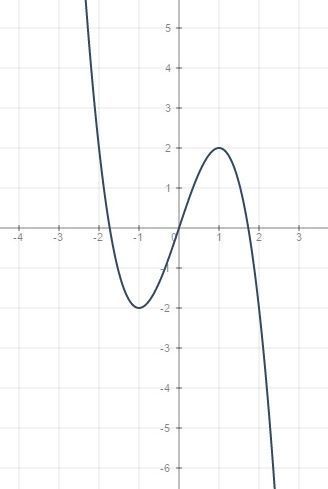
y'=3-3x² y'=0 x²=1 x=-1 x=1
y(-1)=-3+1=-2 минимум
y(1)=3-1=2 максимум
это не парабола а кубическая зависимость.
график у приложен.
y(-1)=-3+1=-2 минимум
y(1)=3-1=2 максимум
это не парабола а кубическая зависимость.
график у приложен.
Приложения:
Автор ответа:
0
y=3x-x³
D(y)∈R
y`=3-3x²
3(1-x)(1+x)=0
x=1 x=-1
_ + _
----------------------(-1)-------------(1)-------------------------
min max
ymin=-3+1=-2
ymax=3-1=2
(-1;-2),(1;2) точки экстремума (или вершины по вашему)
D(y)∈R
y`=3-3x²
3(1-x)(1+x)=0
x=1 x=-1
_ + _
----------------------(-1)-------------(1)-------------------------
min max
ymin=-3+1=-2
ymax=3-1=2
(-1;-2),(1;2) точки экстремума (или вершины по вашему)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: novikovainna94
Предмет: Английский язык,
автор: zdotapo
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: Vladlenprotasov
Предмет: Математика,
автор: amidexter