Предмет: Алгебра,
автор: lizairspring2016
Решите уравнение..........................:
Приложения:
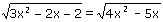
Ответы
Автор ответа:
0
ОДЗ:


возводим обе части в квадрат:






но при x=1 подкоренное выражение в левой части - отрицательно, следовательно х=1 не удовлетворяет ОДЗ.
ответ: х=2
возводим обе части в квадрат:
но при x=1 подкоренное выражение в левой части - отрицательно, следовательно х=1 не удовлетворяет ОДЗ.
ответ: х=2
Автор ответа:
0
ОДЗ
{3x²-2x-2≥0 (1)
{4x²-5x≥0 (2)
1)D=4+24=28
x1=(2-2√7)/6=(1-√7)/3
x2=(1+√7)/3
x<(1-√7)/3 U x>(1+√7)/3
2)x(4x-5)≥0
x=0 x=1,25
x≤0 U x≥1,25
\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////////////////
----------[(1-√7)/3]--------------[0]---------------[(1+√7)/3]-----------[1,25]--------------
///////////////////////////////////////////// \\\\\\\\\\\\\\\\\\\
x∈(-∞;(1-√7)/3] U [1,25;∞)
возведем в квадрат
3x²-2x-2=4x²-5x
4x²-5x-3x²+2x+2=0
x²-3x+2=0
x1+x2=U u x1*x2=2
x1=1∉ОДЗ
х2=2
Ответ х=2
{3x²-2x-2≥0 (1)
{4x²-5x≥0 (2)
1)D=4+24=28
x1=(2-2√7)/6=(1-√7)/3
x2=(1+√7)/3
x<(1-√7)/3 U x>(1+√7)/3
2)x(4x-5)≥0
x=0 x=1,25
x≤0 U x≥1,25
\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////////////////
----------[(1-√7)/3]--------------[0]---------------[(1+√7)/3]-----------[1,25]--------------
///////////////////////////////////////////// \\\\\\\\\\\\\\\\\\\
x∈(-∞;(1-√7)/3] U [1,25;∞)
возведем в квадрат
3x²-2x-2=4x²-5x
4x²-5x-3x²+2x+2=0
x²-3x+2=0
x1+x2=U u x1*x2=2
x1=1∉ОДЗ
х2=2
Ответ х=2
Похожие вопросы
Предмет: История,
автор: gjjj53242
Предмет: Русский язык,
автор: nargizaamonova92
Предмет: Литература,
автор: wekooq
Предмет: Химия,
автор: nastyakonoval