Основания трапеции равны 10 и 6. Найдите длину отрезка, соединяющего середины диагоналей трапеции.
Ответы
Ответ:
Длина отрезка, соединяющего середины диагоналей трапеции=2
Пошаговое объяснение:
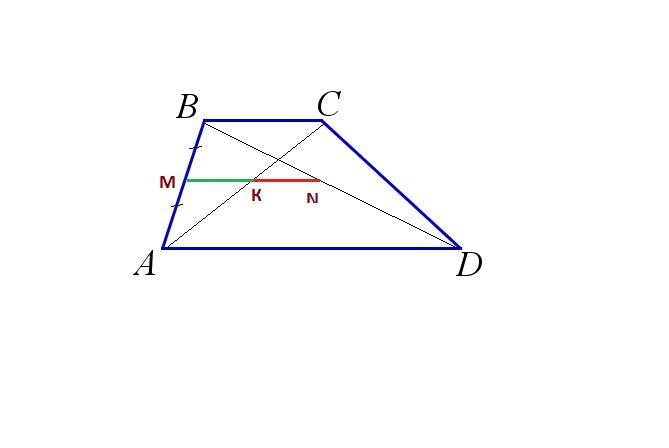
Пусть в трапеции АBCD KN - линия, которая соединяет середины диагоналей. AD=10; ВС=6 - по условию.
На боковой стороне трапеции АВ возьмем точку М -середину этой стороны. Тогда отрезок МК соединяет середины 2-х сторон треугольника АВС и является средней линией, которая параллельна его основанию ВС. МК=1/2* ВС
Отрезок MN также соединяет середины сторон треугольника ACD и является средней линией ΔACD и параллельна его основанию AD. MN=1/2*AD
Т.к. ВС параллельна AD(основания трапеции), то МК и MN также им параллельны и обе проходят через точку М. Известно, что через точку можно провести только одну прямую параллельную другой, следовательно отрезки МК и MN лежат на одной прямой.
Таким образом, КN=MN-МК
КN=1/2*AD-1/2* ВС
КN=1/2*(AD- ВС) КN=1/2*(10-6)
КN=2