Предмет: Математика,
автор: yourmumsboyfriend
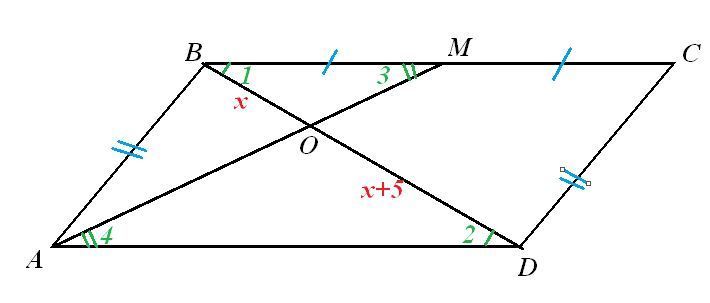
В параллелограмме ABCD точка M - середина стороны BC. AM∩BD=0. Найдите длину диагонали BD, если отрезок OD на 5 больше отрезка BO.
Ответы
Автор ответа:
3
Т.к. ABCD - параллелограмм, то АВ||CD, AD||BC, АВ=CD, AD=BC.
ΔВОМ и ΔAOD подобны по двум углам (накрестлежащие углы: ∠1=∠2, ∠3=∠4).
Отсюда следует:
Т.к. М - середина ВС, то
Получим
2x = x + 5
x = 5
BD = x + x + 5 = 2x + 5 =2·5+5=15.
Ответ: 15.
ΔВОМ и ΔAOD подобны по двум углам (накрестлежащие углы: ∠1=∠2, ∠3=∠4).
Отсюда следует:
Т.к. М - середина ВС, то
Получим
2x = x + 5
x = 5
BD = x + x + 5 = 2x + 5 =2·5+5=15.
Ответ: 15.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: lons81822
Предмет: Математика,
автор: Guuugugugugug
Предмет: Математика,
автор: hexoposhiy
Предмет: История,
автор: martirosan400