Предмет: Математика,
автор: alenavoloshuk
радиус круга вписанного в прямоугольную трапецию с периметром 294 см, равняется 36см. навйдите большую боковую сторону трапеции
Ответы
Автор ответа:
1
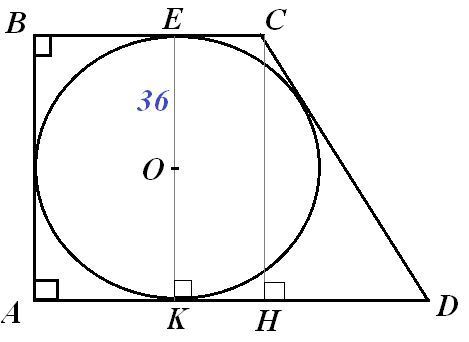
Пусть АВСD - прямоугольная трапеция, О - центр вписанного круга.
CD - большая боковая сторона.
ОЕ=ОК=r=36см. Тогда диаметр ЕК=72см.
По свойству прямоугольной трапеции АВ=ЕК=72см.
По свойству описанной трапеции АВ+СD=BC+AD
По-скольку Р=АВ+ВС+СD+AD=294см, то АВ+СD=BC+AD=294:2=147(см).
АВ+CD=147 см и AB=72см, тогда CD=147-72=75(см).
Ответ: 75см.
CD - большая боковая сторона.
ОЕ=ОК=r=36см. Тогда диаметр ЕК=72см.
По свойству прямоугольной трапеции АВ=ЕК=72см.
По свойству описанной трапеции АВ+СD=BC+AD
По-скольку Р=АВ+ВС+СD+AD=294см, то АВ+СD=BC+AD=294:2=147(см).
АВ+CD=147 см и AB=72см, тогда CD=147-72=75(см).
Ответ: 75см.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: marusjawredina35
Предмет: История,
автор: aleinikovaiona
Предмет: История,
автор: kairgalijkyzya
Предмет: География,
автор: Bolusko
Предмет: Математика,
автор: christinakrasyuk