Предмет: Геометрия,
автор: nabludatel00
Докажите, что в прямоугольном треугольнике биссектриса прямого угла делит угол, образованный высотой и медианой из этого угла, пополам.
Дерзайте!
Ответы
Автор ответа:
0
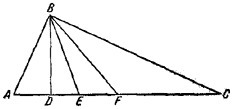
Пусть в ΔΔABC угол ABC прямой, BD — высота, BE — биссектриса и BF — медиана.
Так как BF = FC, то ∠CBF = ∠AСВ. Но
Так как BF = FC, то ∠CBF = ∠AСВ. Но
∠ABD = π/2 — ∠BAD = ∠ACB.
Следовательно, ∠ABD = ∠CBP и
∠DBE = ∠ABE — ∠ABD = ∠CBE — ∠CBF = ∠FBE,
что и требовалось доказать.
Приложения:
nabludatel00:
Только ∠ABD = не ∠CBP, а ∠ABD = ∠CBF, а так все норм....
Похожие вопросы
Предмет: Математика,
автор: vladimirperepelica05
Предмет: Алгебра,
автор: b16900741
Предмет: Обществознание,
автор: natasacom56
Предмет: Английский язык,
автор: doknika26
Предмет: Алгебра,
автор: SIAMK