Предмет: Алгебра,
автор: gaga1701
Математики, помогите пожалуйста найти ошибку, не сходиться с ответом,
Нужно найти сумму корней уравнения, почему не сходиться, желательно подробно!
Приложения:
gaga1701:
Ответ: сумма корней 9, в у меня 8/3
плодить аккаунты нехорошо )ошибка в третьей строчке. правильный ответ 13
Благодарю, но в чем ошибка? За аккаунт извиняюсь и исправлюсь!)
2x^2 как внутри скобки оказалось?
выносите общий множитель за скобки, но 2х^2 не имеет множителей...
Ага, я убрал Ее оттуда, но какой это даст результат? Ещё раз извиняюсь
ну я же уже написал - в лоб не получается ) возможно кто-то предложит способ не раскрывая все скобки.
Я бы сделал как вы, но я не понимаю, когда вы раскрыли, откуда у вас столько получилось
ну довольно нудная работа, раскрытие скобок. ) но раз такие задания даете, предпологалось что это делать умеете ).
Ответы
Автор ответа:
2
удобнее всего сделать замену...
ввести еще одну переменную и
найти зависимость новой переменной от икс))
ввести еще одну переменную и
найти зависимость новой переменной от икс))
Приложения:
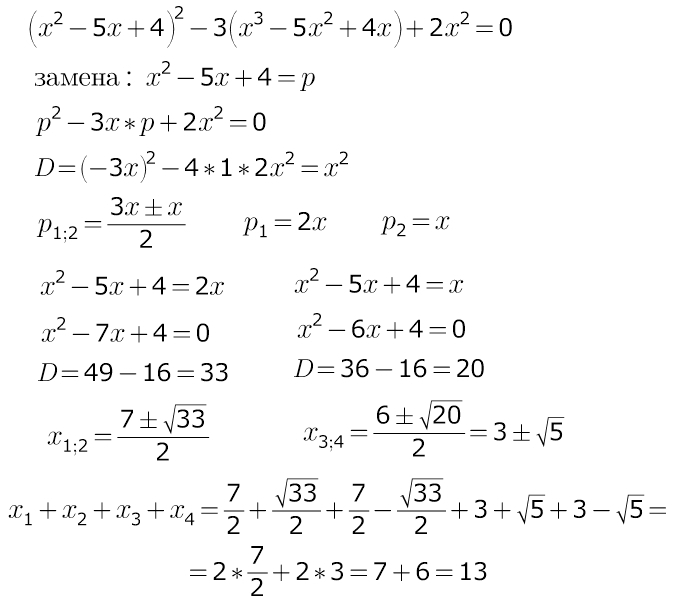
спасибо! здорово! я в другой ипостаси задающего вопрос все скобки раскрывал. так действительно проще
не... скобки раскрывать лениво))) а квадратичная зависимость очевидна...
Благодарю!
Автор ответа:
1
В условии задачи не говорится о действительных корнях.
Найдем коэффициенты при х в четвертой степени очевидно что он равен 1. Первая сводка в квадрате. х^4.
-5х*x^2-x^2*5x*x^2-3x^3 множители содержащие х^3.
=-13х^3.
сумма корней уравнения n-ой степени равно коэффициенты при степени n-1 с обратным знаком. Обобщенная теорема Виета - качается всех корней включая кратные и комплексные. Произведение всех корней равно 16. Если разложить на простые множители то можно получить корни. И если уж очень необходимо проверить смену знака.
Ответ. 13.
Найдем коэффициенты при х в четвертой степени очевидно что он равен 1. Первая сводка в квадрате. х^4.
-5х*x^2-x^2*5x*x^2-3x^3 множители содержащие х^3.
=-13х^3.
сумма корней уравнения n-ой степени равно коэффициенты при степени n-1 с обратным знаком. Обобщенная теорема Виета - качается всех корней включая кратные и комплексные. Произведение всех корней равно 16. Если разложить на простые множители то можно получить корни. И если уж очень необходимо проверить смену знака.
Ответ. 13.
Вот это да ! Самое правильное решение!!! Виетта только конечно )
писал с планшета, потому опечатки буковки мелкие
Прошу прощения, но это решение не годится, если рассматриваются только действительные решения. Ведь существование четырех действительных решений не доказано! Пример. Уравнение x^4+1=0 не имеет действительных решений, поэтому теорема Виета не применима. Кроме того, из условия не совсем понятно, нужно ли учитывать кратные корни столько раз, какова их кратность. Например, (x-1)^4=0 имеет один корень x=1, но его кратность равна 4. Теорема Виета для этого уравнения дала бы ответ: сумма корней равна 4
Тогда достаточно еще проверить что рациональных корней нет +- 1 +- 2 +-4 +- 8 +- 16 Иррациональные корни парами не ходят
А как с (x^2-2)^2=0?
А ну да 4 степени же...
А вдруг часть корней или все корни комплексные?
Читайте условие в нем ничего не говорится о действительных корнях. Что касается теоремы Виета она касается всех корней и каждый корень берется столько раз какова его кратность.
в крайнем случае у вас в этом уравнении может быть либо 2 либо 4 комплексных корня.
В школьной задаче речь по умолчанию идет о действительных корнях. А когда корень кратный, многие считают, что он единственный. Например, в уравнении x^2-2x+1=0 оба корня равны 1, их сумма равна 2, что и дает теорема Виета. Однако многие учителя и школьники за ними будут говорить, что корень один и значит в ответе нужно записать не 2, а 1. Я не говорю, что это хорошо. Я считаю, что это плохо, но это так.
Похожие вопросы
Предмет: Психология,
автор: gordienkonasta82
Предмет: Қазақ тiлi,
автор: shapovalovartyom7
Предмет: История,
автор: olshanskayulia201020
Предмет: Математика,
автор: Esenia2929
Предмет: Математика,
автор: mixeevakris