Question

Периметр правильного трикутника, вписаного в коло, дорівнює 6√3 см. Знайти площу квадрата, описаного навколо кола.

Answer 1

S- площадь. S=a². Значит: чтобы найти площадьнадо найти сторону(а).
Периметр правильного треугольника=6√3. А периметр правильного треугольника равен: Р=3с, где с- сторона треугольника. Значит сторона треугольника равна: Р/3=6√3/3=2√3. Теперь надо найти радиус описанной окружности, то есть R. Пользуясь формулой R=с/√3, можно легко найти R.
R=2√3/√3=2. А чтобы найти сторону квадрата(а), надо воспользоваться формулой: R=a/√2, тогда: а=√2R=√2*2=2√2. A S(площадь квадрата)=(2√2)²=
4*2=8. Ответ: Площадь квадрата равна 8 см).

Answer 2

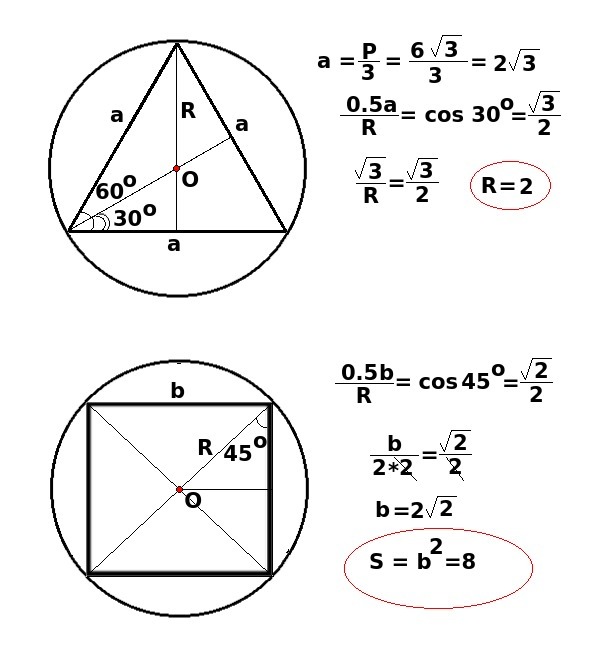
Решение на рисунке!!!

Ответ S=8