Question

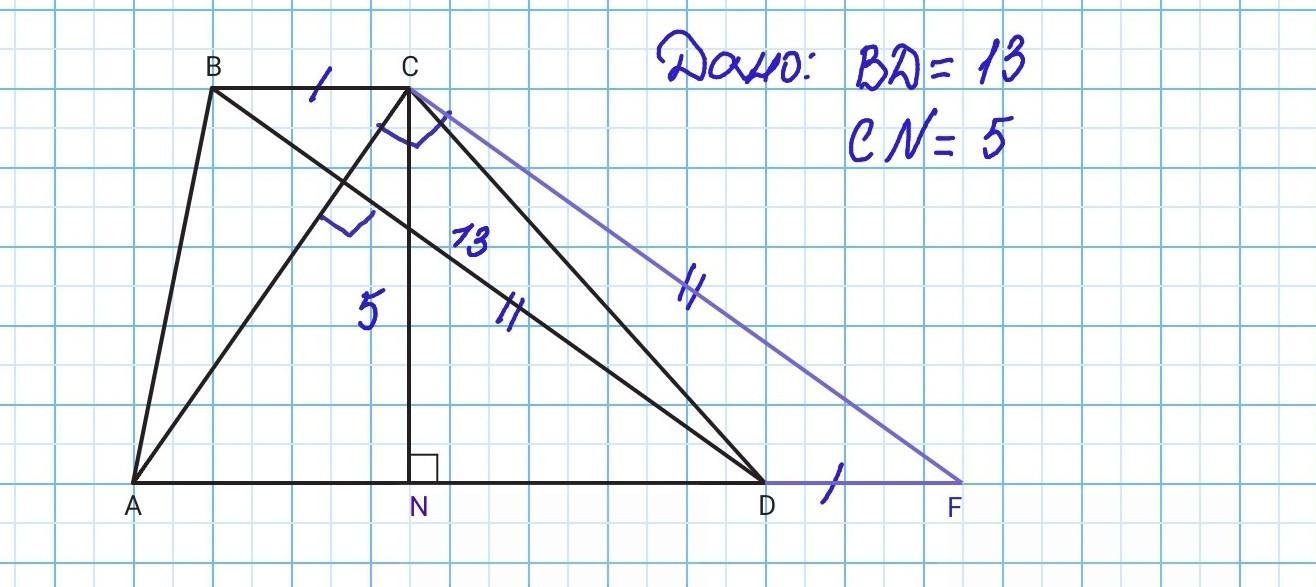
диагонали трапеции взаимно перпендикулярны. Одна из них равна 13, а высота трапеции равна 5. Найдите значение выражения 24 S, где S- площадь трапеции

Answer 1

Ответ:

845 кв ед

Объяснение:

Обычно, когда диагонали трапеции перпендикулярны, решить задачу поможет дополнительное построение: проведём через вершину C меньшего основания BC прямую CF, параллельную диагонали BD.

Четырехугольник BCFD — параллелограмм, так как: CF II BD по построению, BC II AD как основания трапеции). =>DF=BC, CF=BD=13

Так как диагонали трапеции перпендикулярны, то CF ⟂ AC  (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой). Треугольник ACF - прямоугольный. <ACF=90° .

Проведем высоту трапеции CN. По теореме Пифагора найдём катет NF в прямоугольном треугольнике АСF:

$NF = \sqrt{ {CF}^{2} - {CN}^{2} } = \sqrt{ {13}^{2} - {5}^{2} } = \\ = \sqrt{169 - 25} = \sqrt{144} = 12$

В прямоугольном треугольнике ACF CN — высота, проведенная к гипотенузе.  

Пропорциональные отрезки в прямоугольном треугольнике связаны соотношениями:

$CN = \sqrt{AN \times NF} \: = > 5 = \sqrt{AN \times 12} \\ \\ 25 = AN \times 12 \: = > \: AN = \dfrac{25}{12}$

$CF = \sqrt{NF \times AF} \: = > \: 13 = \sqrt{12 \times AF} \\ \\ 169 = 12 \times AF \: = > \: AF = \dfrac{169}{12}$

$AC \: = \sqrt{AN \times AF} = \sqrt{ \dfrac{25}{12} \times \dfrac{169}{12} } = \dfrac{5 \times 13}{12} = \dfrac{65}{12}$

Поскольку диагонали трапеции перпендикулярны, то площадь трапеции можно найти по формуле:

$S = \dfrac{1}{2} \times d_1 \times d_2 = \dfrac{1}{2} \times AC \times BD = \\ \\ = \dfrac{1}{2} \times \dfrac{65}{12} \times 13 = \dfrac{845}{24}$

Значение выражения 24S будет равно:

$24S = 24 \times \dfrac{845}{24} = 845$