Предмет: Математика,
автор: dustovoi
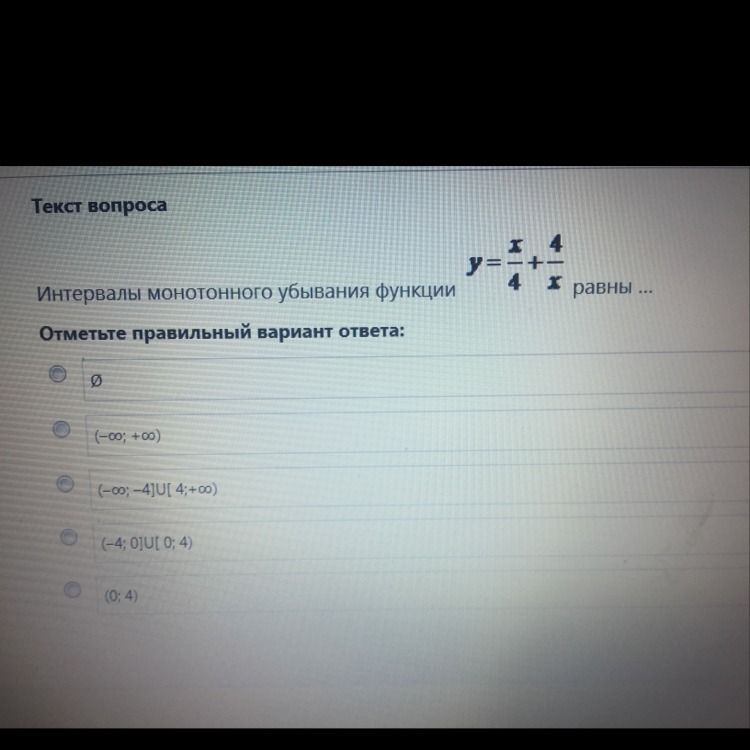
Интервалы монотонного убывания функции
Приложения:
Ответы
Автор ответа:
0
Производная функции равна:
y' = (1/4) - (4/x²) =((x-4)(x+4))/4x².
Получили 2 критические точки: х = -4 и х = 4.
Находим значения производной вблизи этих точек:
x = -5 -4 -3 3 4 5
y' = 0,09 0 -0,1944 -0,1944 0 0,09.
Где производная отрицательна - там функция убывает ( с учётом того, что при х = 0 функция терпит разрыв): (-4; 0) ∪ (0; 4).
y' = (1/4) - (4/x²) =((x-4)(x+4))/4x².
Получили 2 критические точки: х = -4 и х = 4.
Находим значения производной вблизи этих точек:
x = -5 -4 -3 3 4 5
y' = 0,09 0 -0,1944 -0,1944 0 0,09.
Где производная отрицательна - там функция убывает ( с учётом того, что при х = 0 функция терпит разрыв): (-4; 0) ∪ (0; 4).
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Литература,
автор: anastasiaodarenko200
Предмет: Алгебра,
автор: venomggg777
Предмет: Биология,
автор: LondraYET
Предмет: Литература,
автор: vita344