Question

Треугольник AМР равнобедренный. Треугольник APR равнобедренный. АР - общее основание. Доказать, что треугольник MPR равен треугольнику MAR.

Answer 1

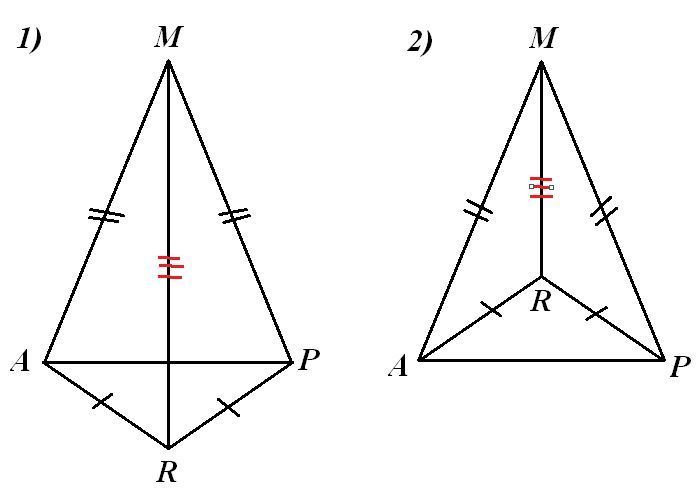
Чертеж во вложении.
Поскольку в условии не описано точное положение вершин М и R равнобедренных треугольников АМР и ARP относительно их общего основания АР, то  и рассматривать надо два случая, представленные двумя чертежами 1) и 2). Но решение в обоих случаях одинаковое.

Т.к. ΔАМР - равнобедренный (по условию), то АМ=РМ. Т.к. ΔАRР - равнобедренный (по условию), то АR=РR.
Рассмотрим ΔМAR и ΔМРR. У них:
1) МА=МР (по доказанному)
2) RA=RP (по доказанному)
3) MR - общая.
Таким образом, ΔМAR = ΔМРR по трем сторонам.
Доказано.