Предмет: Математика,
автор: RedOwl99
Помогите решить олимпиаду (4)
Приложения:
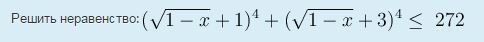
Ответы
Автор ответа:
1
Область определения: x <= 1
Замена
(y - 1)^4 + (y + 1)^4 <= 272
y^4 - 4y^3 + 6y^2 - 4y + 1 + y^4 + 4y^3 + 6y^2 + 4y + 1 <= 272
2y^4 + 12y^2 + 2 <= 272
Делим все на 2 и переносим 272 влево
y^4 + 6y^2 - 135 <= 0
(y^2 + 15)(y^2 - 9) <= 0
y^2 + 15 > 0 при любом y, поэтому
y^2 - 9 = (y + 3)(y - 3) <= 0
Обратная замена
(√(1-x) + 2 + 3)(√(1-x) +2 - 3) <= 0
(√(1-x) + 5)(√(1-x) - 1) <= 0
Корень арифметический, то есть неотрицательный, поэтому 1 скобка положительна при любом x < 1. Остается
√(1 - x) - 1 <= 0
√(1 - x) <= 1
1 - x <= 1
x >= 0
Но, по области определения x <= 1. Поэтому
Ответ: x ∈ [0; 1]
Замена
(y - 1)^4 + (y + 1)^4 <= 272
y^4 - 4y^3 + 6y^2 - 4y + 1 + y^4 + 4y^3 + 6y^2 + 4y + 1 <= 272
2y^4 + 12y^2 + 2 <= 272
Делим все на 2 и переносим 272 влево
y^4 + 6y^2 - 135 <= 0
(y^2 + 15)(y^2 - 9) <= 0
y^2 + 15 > 0 при любом y, поэтому
y^2 - 9 = (y + 3)(y - 3) <= 0
Обратная замена
(√(1-x) + 2 + 3)(√(1-x) +2 - 3) <= 0
(√(1-x) + 5)(√(1-x) - 1) <= 0
Корень арифметический, то есть неотрицательный, поэтому 1 скобка положительна при любом x < 1. Остается
√(1 - x) - 1 <= 0
√(1 - x) <= 1
1 - x <= 1
x >= 0
Но, по области определения x <= 1. Поэтому
Ответ: x ∈ [0; 1]
RedOwl99:
Спасибо большое! Вы меня сегодня очень выручаете!
Похожие вопросы
Предмет: Литература,
автор: 30072008xxxtolmachev
Предмет: Химия,
автор: anastasiafyt66
Предмет: Биология,
автор: yakubenkooleg9
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: 1471urdjar