Предмет: Геометрия,
автор: andriyyusko93
сторони трикутника 5 м, 6 м, 7 м. Знайти висоту трикутника проведену до сторони довжиною 6 м.
Ответы
Автор ответа:
0
Высота к стороне 6 м равна:
h = 2√(p(p-a)(p-b)(p-c))/6.
Полуппериметр р = (5+6+7)/2 = 18/2 = 9 м.
h =2√(9*4*3*2)/6 = 2√216/6 = 2*3√24/6 = √24 ≈ 4,89898 м.
h = 2√(p(p-a)(p-b)(p-c))/6.
Полуппериметр р = (5+6+7)/2 = 18/2 = 9 м.
h =2√(9*4*3*2)/6 = 2√216/6 = 2*3√24/6 = √24 ≈ 4,89898 м.
Автор ответа:
0
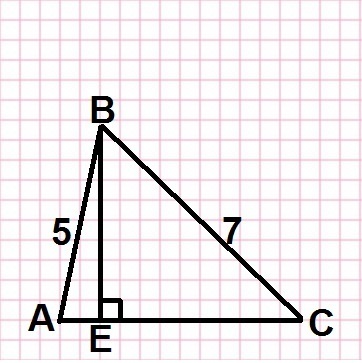
В треугольнике ABC:
AB = 5
AC = 6
BC = 7
BE - высота, опущенная на сторону AC
AE + CE = 6
AE = 6 - CE
В прямоугольном треугольнике ABE:
AE u BE - катеты
Гипотенуза AB = 5
По теореме Пифагора:
AB² = AE² + BE²
BE² = AB² - AE²
В прямоугольном треугольнике BCE:
BE u CE - катеты
Гипотенуза BC = 7
По теореме Пифагора:
BC² = BE² + CE²
BE² = BC² - CE²
⇒ AB² - AE² = BC² - CE²
5² - (6 - CE)² = 7² - CE²
25 - 36 + 12CE - CE² = 49 - CE²
12CE = 49 + 11
12CE = 60
CE = 5 (м)
По теореме Пифагора:
BC² = BE² + CE²
BE² = BC² - CE²
BE² = 7² - 5²
BE² = 49 - 25
BE² = 24
BE = √24
BE = 2√6 (м)
AB = 5
AC = 6
BC = 7
BE - высота, опущенная на сторону AC
AE + CE = 6
AE = 6 - CE
В прямоугольном треугольнике ABE:
AE u BE - катеты
Гипотенуза AB = 5
По теореме Пифагора:
AB² = AE² + BE²
BE² = AB² - AE²
В прямоугольном треугольнике BCE:
BE u CE - катеты
Гипотенуза BC = 7
По теореме Пифагора:
BC² = BE² + CE²
BE² = BC² - CE²
⇒ AB² - AE² = BC² - CE²
5² - (6 - CE)² = 7² - CE²
25 - 36 + 12CE - CE² = 49 - CE²
12CE = 49 + 11
12CE = 60
CE = 5 (м)
По теореме Пифагора:
BC² = BE² + CE²
BE² = BC² - CE²
BE² = 7² - 5²
BE² = 49 - 25
BE² = 24
BE = √24
BE = 2√6 (м)
Приложения:
Похожие вопросы
Предмет: Биология,
автор: 1981satrap
Предмет: История,
автор: mirgorod441
Предмет: География,
автор: margaritsarik180
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: Rhi6