Предмет: Алгебра,
автор: 1pc1
Помогите, пожалуйста, решить! :) № 26 (а, в, д), №27 (а, в,д), №28 (а, в, д) и №36.
Приложения:

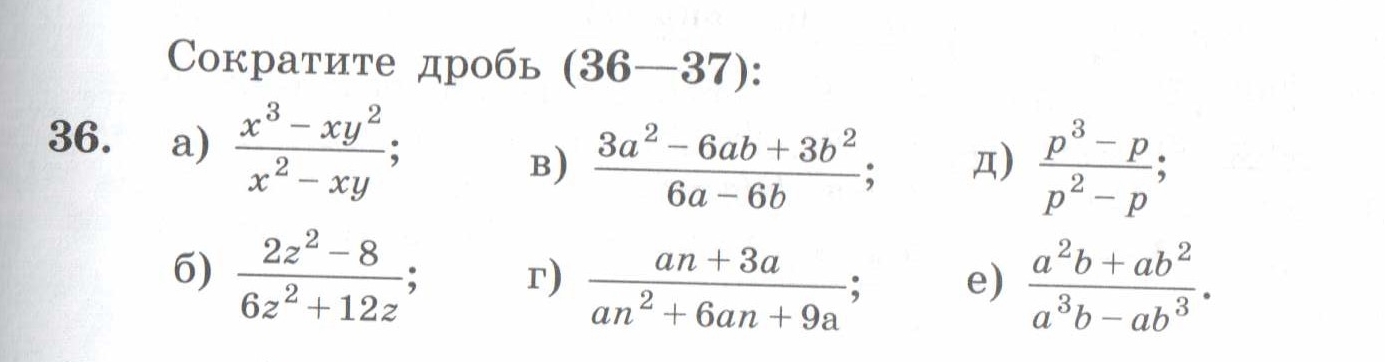
Ответы
Автор ответа:
0
№26(а,в,д)
а)
в)
д)
№27(а,в,д)
a)
в)
д)
№28(а,в,д)
а)
в)
д)
№36
а)
б)
в)
г)
д)
е)
а)
в)
д)
№27(а,в,д)
a)
в)
д)
№28(а,в,д)
а)
в)
д)
№36
а)
б)
в)
г)
д)
е)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: shushakovaalisa
Предмет: Английский язык,
автор: adiakop
Предмет: Геометрия,
автор: xfg